Assertion (A): In prism, higher the refractive index, lower will be the angle of deviation. Reason (R): The angle of deviation is inversely proportional to the
Both A and R are true, and R is the correct explanation of A.
Both A and Rare true, but is not the correct explanation of A
A is true but R is false
A is false but R is true.
The correct Answer is:C
For a given angle of incidence, the prism with higher refractive index produces a greater deviation than the prism which has a lower refractive index. Thus, the angle of deviation increases with an increase in the refractive index of the medium.
Related Theory
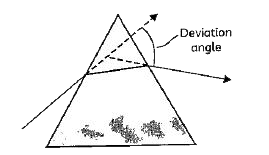
Light is deflected as it enters a material with refractive index >1 ray of light is deflected twice in a prism . The sum of these deflections is the deviation angle
Similar Questions
The refractive index of the material of prism √3, then the angle of minimum deviation of prism is
View Solution(a) If the refracting angle of a prism is 60∘ and the minimum deviation is 30∘, then find the angle of incidence.
(b) A ray of light passes through an equilateral prism such that the angle of emergence is equal to the angle of incidence and each is equal to 3/4th of the angle of prism. Find the angle of deviation.
(c) The refracting of a prism is A and the refractive index of the material of the prism is cotA/2. Find the angle of deviation.
(d) The angle of a prism is 60∘. What is the angle of incidence for minimum deviation? The refractive index of the material of the prism is √2.
View Solution
Knowledge Check
The refracting angle of a prism is A and refractive index of material of prism is cot(A2) The angle of minimum deviation is
A(180∘−3A)B(180∘+2A)C(90∘−A)D(180∘−2A)If a prism having refractive index √2 has angle of minimum deviation equal to the angle of refraction of the prism, then the angle of refraction of the prism is:
A30∘B45∘C60∘D90∘For a prism of refractive index 1.732, the angle of minimum deviation is equal to the angle of the prism. The angle of the prism is
A80∘B70∘C60∘D50∘
If a prism having refractive index √2 has angle of minimum deviation equal to the angle of refraction of the prism, then the angle of refraction of the prism is:
View SolutionFor a prism of refractive index 1.732, the angle of minimum deviation is equal to the angle of the prism. The angle of the prism is
View SolutionThe refracting angle of a prism is A, and refractive index of the material of the prism is cot(A2). The angle of minimum deviation is
View SolutionThe minimum deviation on a prism of refractive index √3 is equal to the angle of prism. Find the angle of the prism.
View SolutionThe refracting angle of a prism is A and refractive index of the material of the prism is cos(A/2). The angle of minimum deviation is
View Solution
