ΔABC तथा ΔDEF में, ABDE=BCDF ये दोनों त्रिभुज समरूप होंगे, यदि
∠B=∠E
∠A=∠D
∠B=∠D
∠A=∠F
The correct Answer is:C
Topper's Solved these Questions
- त्रिभुज BOOK - BHARATI BHAWANCHAPTER - त्रिभुज EXERCISE - प्रश्नमाला 7D
16 Videos
- त्रिकोणमितीय सर्वसमिकाएँ BOOK - BHARATI BHAWANCHAPTER - त्रिकोणमितीय सर्वसमिकाएँ EXERCISE - प्रश्नमाला 13C (बहुवैकल्पिक प्रश्न )
20 Videos
- दो चरों वाले रैखिक समीकरण - युग्म BOOK - BHARATI BHAWANCHAPTER - दो चरों वाले रैखिक समीकरण - युग्म EXERCISE - प्रश्नमाला 3F (बहुवैकल्पिक प्रश्न)
27 Videos
Similar Questions
कुछ त्रिभुजों की भुजाओं के माप नीचे दिए गए हैं। ज्ञात कीजिए कि इनमें कौन-कौन समकोण त्रिभुज हैं?
9 cm, 16 cm, 18cm
View Solutionयदि sinA+sin2A=1 है, तो व्यंजक (cos2A+cos4A) का मान है
View Solutionयदि 2 x + 3y = 12 तथा 3 x - 2y = 5 है, तो
View SolutionΔABC तथा ∠DEF में, AB = DE तथा BC = EF है, तब ज्ञात हुआ की ΔABC≅ΔDEF, तब।
View SolutionIf in ΔABCandΔDEF , ABDE=BCFD, then they will be similar, when
View SolutionIn ΔABCandΔDEF, it is given that AB = DE and BC = EF. In order that ΔABC≅ΔDEF, we must have
View SolutionΔABC और ΔDEF दो त्रिभुज इस प्रकार है कि AB,BC क्रमशः DE,EF के समांतर और बराबर है। दिखाइए कि AC,DF के बराबर और समांतर है।
View SolutionΔABC~ΔDEF, then ABDE=……….EF
View Solutionत्रिभुज ABC व ΔDEFदो त्रिभुज इस प्रकार हैं कि AC=2.5सेमी. BC=5सेमी. तथा DE=2.5सेमी., DF=5 सेमी व ∠D=75 व ∠ C =75 क्या ये दोनों त्रिभुज सर्वांगसम होंगे ?
View SolutionIn ΔABC and ΔDEF if ABDE=BCDF=ACEF, then-
View SolutionΔABC~ΔDEF and in ΔABC and ΔDEF, the corresponding sides of AB, BC and CA are DE, EF and DF respectively. If ∠A=47∘ and ∠E=83∘, then find the value of ∠C.
View SolutionΔABC और ΔDEF में, ABDE=BCFD तो ये त्रिभुज समरूप होंगे यदि
View SolutionDeltaABC And DeltaDEF In AB||=DE And BC||=EF . Prove that AC||=DF
View SolutionIn ΔABC and ΔDEF, AB= DE, AB || DE, BC= EF and BC|E|F. Vertices A, B and C are joined to vertices D, E and F respectively. Show that
AC= DF
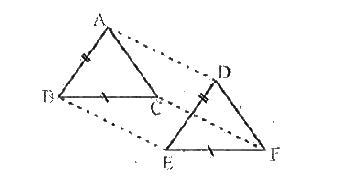
View SolutionIn ΔABC and ΔDEF, AB= DE, AB || DE, BC= EF and BC|E|F. Vertices A, B and C are joined to vertices D, E and F respectively. Show that
ΔABC≅ΔDEF.
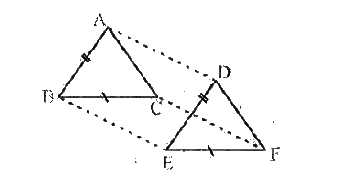
View SolutionIn ΔABCandΔDEF,AB=DE,AB||DE,BC=EFandBC||EF Vertices A,B and C are joined to vertices D , E and F respectively show that
quadrilateral ABED is a parallelogram
quadrilateral BEFC is a parallelogram
AD∣∣CFandAD=CF
quadrilateral ACFD is a parallelogram
AC=DF
ΔABC≈ΔDEF.
View Solution
