The circumferences of the fore and hind wheels of a carriage are metres and meters respectively .At any given moment a chalk mark is put on the point of contact of each wheel with the ground. Find the distance travelled by the carriage so that both the chalk marks are again on the ground at the same time-
218 m
m
m
217 m
The correct Answer is:B
To solve the problem of finding the distance traveled by the carriage so that both chalk marks are again on the ground at the same time, we will follow these steps:
Step 1: Convert the Circumferences to Improper Fractions
The circumferences of the fore and hind wheels are given as:
- Fore wheel: 6314=6×14+314=84+314=8714 meters
- Hind wheel: 8118=8×18+118=144+118=14518 meters
Step 2: Find the LCM of the Circumferences
To find the distance traveled by the carriage when both wheels have completed a whole number of rotations, we need to calculate the LCM of the two circumferences:
- LCM of 8714 and 14518
Using the formula for LCM of two fractions:
LCM(ab,cd)=LCM(a,c)HCF(b,d)
where a=87, b=14, c=145, and d=18.
Step 3: Calculate LCM of Numerators
We need to find the LCM of 87 and 145.
- Prime factorization:
- 87=3×29
- 145=5×29
The LCM will be:
LCM(87,145)=3×5×29=435
Step 4: Calculate HCF of Denominators
Next, we find the HCF of 14 and 18:
- Prime factorization:
- 14=2×7
- 18=2×32
The HCF will be:
HCF(14,18)=2
Step 5: Calculate the LCM of the Circumferences
Now we can calculate the LCM of the circumferences:
LCM(8714,14518)=4352
Step 6: Convert to Decimal
To find the distance in meters:
4352=217.5 meters
Final Answer
The distance traveled by the carriage so that both chalk marks are again on the ground at the same time is 217.5 meters.
---
The circumferences of the fore and hind wheels are given as:
- Fore wheel: 6314=6×14+314=84+314=8714 meters
- Hind wheel: 8118=8×18+118=144+118=14518 meters
To find the distance traveled by the carriage when both wheels have completed a whole number of rotations, we need to calculate the LCM of the two circumferences:
- LCM of 8714 and 14518
LCM(ab,cd)=LCM(a,c)HCF(b,d)
where a=87, b=14, c=145, and d=18.
We need to find the LCM of 87 and 145.
- Prime factorization:
- 87=3×29
- 145=5×29
LCM(87,145)=3×5×29=435
Next, we find the HCF of 14 and 18:
- Prime factorization:
- 14=2×7
- 18=2×32
HCF(14,18)=2
Now we can calculate the LCM of the circumferences:
LCM(8714,14518)=4352
To find the distance in meters:
4352=217.5 meters
The distance traveled by the carriage so that both chalk marks are again on the ground at the same time is 217.5 meters.
Topper's Solved these Questions
Similar Questions
The radii of the front wheel and the rear wheel of a bike are 14 cm and 21 cm respectively. Rahul puts a red mark on the point of contact of each of the wheels with the ground when the bike is stationary. Once the bike start moving, then after what distance will the two red marks touch the ground again simultaneously? (a) 42 cm (b) 84 cm (c) 264 cm (d) 294 cm
View SolutionThe fore wheel of a carriage makes 6 revolutions more than the rear wheel in going 120m. If the diameter of the fore wheel be increased by 14 its present diameter and the diameter of the rear wheel be increased by one-fifth of its present diameter, then the fore wheel makes 4 revolutions more than the rear wheel in going the same distance. Find the circumference of each wheel of the carriage.
View Solution
Knowledge Check
The cicumferences of a fore and hind wheels of a carriage are 6314m and 8118m respectively. At any given moment, a chalk mark is put on the point of contact of each wheel with the ground. Find the distance travlled by the carriage so that both the chalk marks are again on the ground at the same time
A218mB217.5mC218.25mD217mAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What are main 3 components in a Roget's spiral?
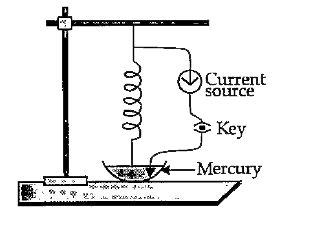 AMarcury, AC voltage sourceBMercury, DC voltage sourceCMercury, DC voltage source, keyDMercury, AC voltage source, key
AMarcury, AC voltage sourceBMercury, DC voltage sourceCMercury, DC voltage source, keyDMercury, AC voltage source, key
Case 1: If you take a ball and push it so that it rolls across a smooth, cemented floor. Wait for the ball to stop by itself. Mark the point at which it stopped by drawing a line on the floor with chalk powder. Measure the distance travelled by the ball using a measuring tape.
Case 2: If you take the same ball and push it the same way as before on a sandy ground. Again, measure the distance travelled by the ball.

What do you understand about frictional force in this case?
View SolutionThe fore wheel of a carriage makes 6 revolution more than the rear wheel in going 120 m. if the diameter of the for wheel be increases 14 its present diameter and the diameter of the rear wheel be increasesby one fifth of its present diameter then the four wheel makes 4 going its same distance. Find the circumference of four wheel of the carriage.
View SolutionCase 1: If you take a ball and push it so that it rolls across a smooth, cemented floor. Wait for the ball to stop by itself. Mark the point at which it stopped by drawing a line on the floor with chalk powder. Measure the distance travelled by the ball using a measuring tape.
Case 2: If you take the same ball and push it the same way as before on a sandy ground. Again, measure the distance travelled by the ball.

In which case, ball will stop first by itself?
View SolutionTwo wheels, each marked with a dot on its rim, are mounted side by side. Initially the dots are alinged and wheels are at rest. One of the wheels is given a constant angular acceleration of (π/2)rad/sec2 and the other wheel is given a constant angular acceleration (π/4)rad/sec2. Both acceleration are in the same direction. Find the time (in s) after which the two dots will becomes alingned again for the first time.
View SolutionTwo balls of the same radius and weight are suspended on threads so that their surface are in contact. A charge of q0=4×10−7C is given to the balls which makes them repel each other and diverge to an angle of 60°. Find the mass of the balls if the distance of balls from the point of suspension to the centre of ball is 20cm. Find the density of the material of the balls if the angle of divergence becomes 54° when the balls are immersed in kerosene of density 800kgm−3 dielectric constant ofkerosene is εr=2[1.592g,255K/gm3]
View SolutionIn this section each item consists of six sentences of a passage. The first and sixth sentences are given in the beginning as S1 and S6. The middle four sentences in each have been jumbled up and labelled P, Q, R and S. You are required to find the proper sequence of the four sentences and mark your response accordingly on the Answer Sheet.
S1 : There have been two schools of thought which deal with the errors of learners.
S6 : Both views are popular today but the second is gaining ground fast.
P : The philosophy of the second school is that errors are natural and they will occur in any learning.
Q : So errors, they say, is a sign of faulty teaching methods.
R : The first school maintains that if teaching methods are perfect, errors will never occur.
S : They argue that we should concentrate on how to deal with errors, instead of on method of teaching.
The correct sequence should be (a) Q S R P (b) P S Q R (c)!Q P S R (d) R Q P S
View Solution