During free fall the total energy at 3/4th the height is .....
constant
zero
gravitational potential energy at the top
3/4th the initial potential energy.
The correct Answer is:A
To solve the question regarding the total energy during free fall at three-fourths the height, we need to understand the concepts of potential energy and kinetic energy.
1. Understanding Total Energy:
- The total mechanical energy (E) of an object in free fall is the sum of its gravitational potential energy (PE) and kinetic energy (KE).
- Mathematically, this can be expressed as:
E=PE+KE
2. Potential Energy at Height:
- The potential energy (PE) of an object at a height h is given by the formula:
PE=mgh
- Here, m is the mass of the object, g is the acceleration due to gravity, and h is the height from the ground.
3. Total Energy at the Top:
- At the top of the fall (height h), the object has maximum potential energy and zero kinetic energy (since it is at rest).
- Therefore, the total energy at the top is:
E=mgh+0=mgh
4. Free Fall to Three-Fourths Height:
- When the object falls to three-fourths of the height, the height h′ is:
h′=34h
- The potential energy at this height is:
PE′=mg(34h)=34mgh
5. Kinetic Energy at Three-Fourths Height:
- As the object falls, its potential energy is converted into kinetic energy. At three-fourths the height, the total energy remains constant (as established earlier).
- Thus, the kinetic energy (KE) at this height can be calculated as:
KE′=E−PE′=mgh−34mgh=14mgh
6. Total Energy at Three-Fourths Height:
- The total energy at three-fourths of the height is still equal to the total energy at the top:
E=mgh
Conclusion:
The total energy during free fall at three-fourths the height is constant and equal to mgh.
Answer:
The correct option is that the total energy at three-fourths the height is constant.
---
- The total mechanical energy (E) of an object in free fall is the sum of its gravitational potential energy (PE) and kinetic energy (KE).
- Mathematically, this can be expressed as:
E=PE+KE
- The potential energy (PE) of an object at a height h is given by the formula:
PE=mgh
- Here, m is the mass of the object, g is the acceleration due to gravity, and h is the height from the ground.
- At the top of the fall (height h), the object has maximum potential energy and zero kinetic energy (since it is at rest).
- Therefore, the total energy at the top is:
E=mgh+0=mgh
- When the object falls to three-fourths of the height, the height h′ is:
h′=34h
- The potential energy at this height is:
PE′=mg(34h)=34mgh
- As the object falls, its potential energy is converted into kinetic energy. At three-fourths the height, the total energy remains constant (as established earlier).
- Thus, the kinetic energy (KE) at this height can be calculated as:
KE′=E−PE′=mgh−34mgh=14mgh
- The total energy at three-fourths of the height is still equal to the total energy at the top:
E=mgh
The total energy during free fall at three-fourths the height is constant and equal to mgh.
The correct option is that the total energy at three-fourths the height is constant.
Topper's Solved these Questions
- WORK,POWER AND ENERGY BOOK - ICSECHAPTER - WORK,POWER AND ENERGY EXERCISE - NUMERICAL BASED MCQ
17 Videos
- WORK,POWER AND ENERGY BOOK - ICSECHAPTER - WORK,POWER AND ENERGY EXERCISE - DIAGRAM BASED MCQ
3 Videos
- WORK,POWER AND ENERGY BOOK - ICSECHAPTER - WORK,POWER AND ENERGY EXERCISE - DIAGRAM BASED MCQ
3 Videos
- SPECTRUMBOOK - ICSECHAPTER - SPECTRUMEXERCISE - TYPE 3 DIAGRAM BASED MCQ:
5 Videos
Similar Questions
At a height H from the surface of earth, the total energy of a satellite is equal to the potential energy of a body of equal mass at a height 3R from the surface of the earth (R = radius of the earth). The value of H is
View SolutionVictoria falls in Africa is 122 m in height. Calculate the rise in temperature of the water if all the potential energy lost in the fall is converted into heat.
View Solution
Knowledge Check
A raindrop falling from a height h above ground, attains a near terminal velocity when it has fallen through a height (3/4)h. Which of the diagrams shown in figure correctly shows the change in kinetic and potential energy of the drop during its fall up to the ground ?
A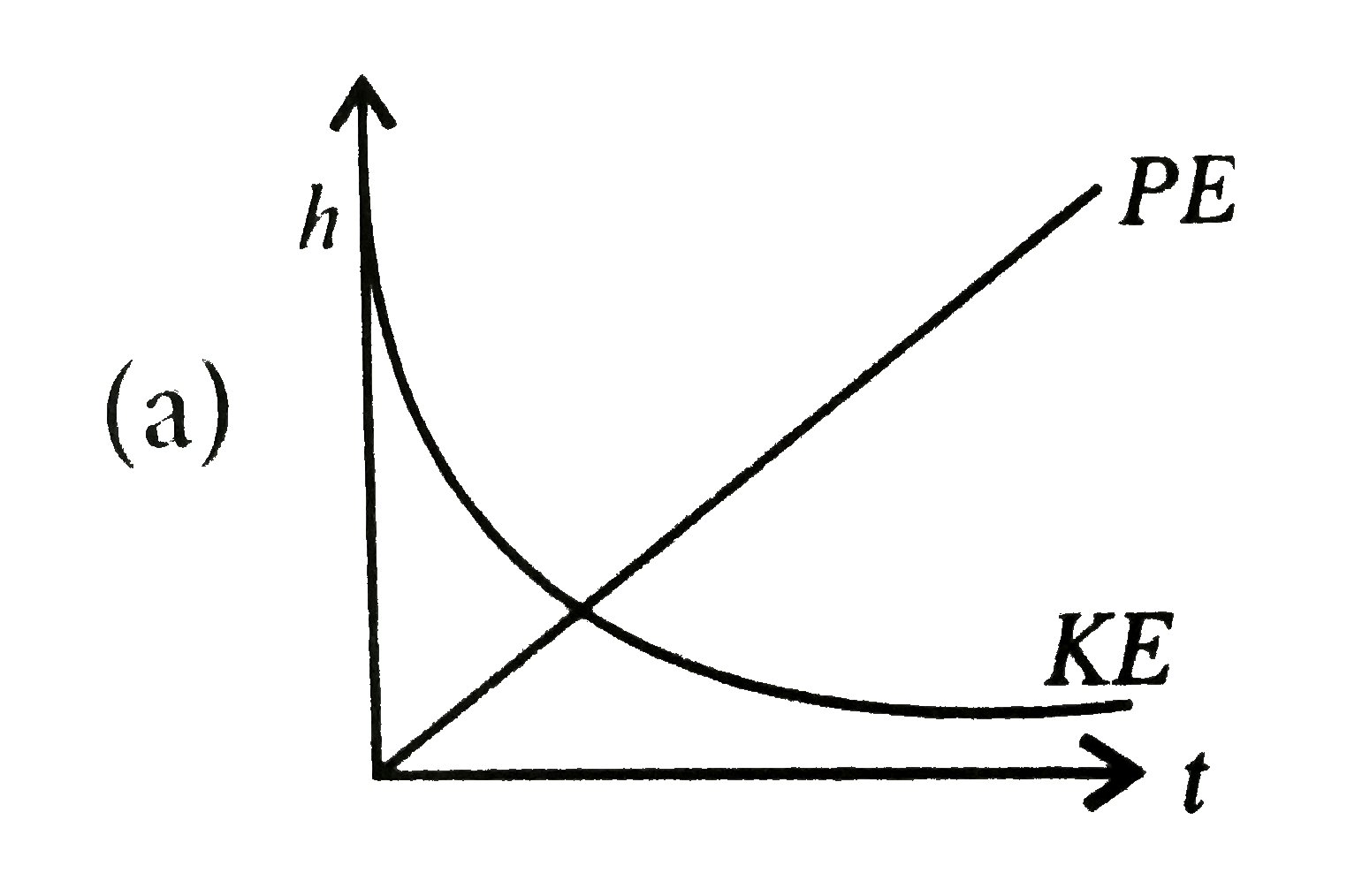 B
B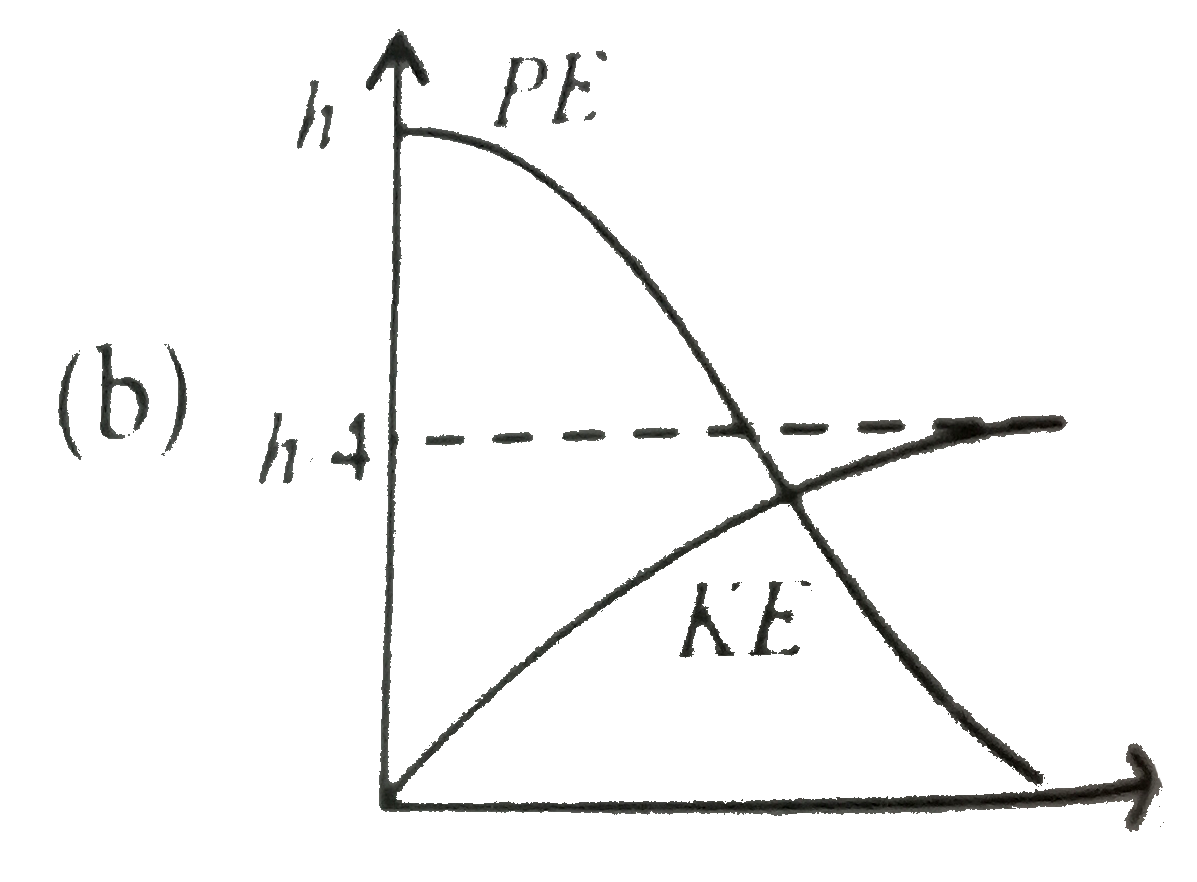 C
C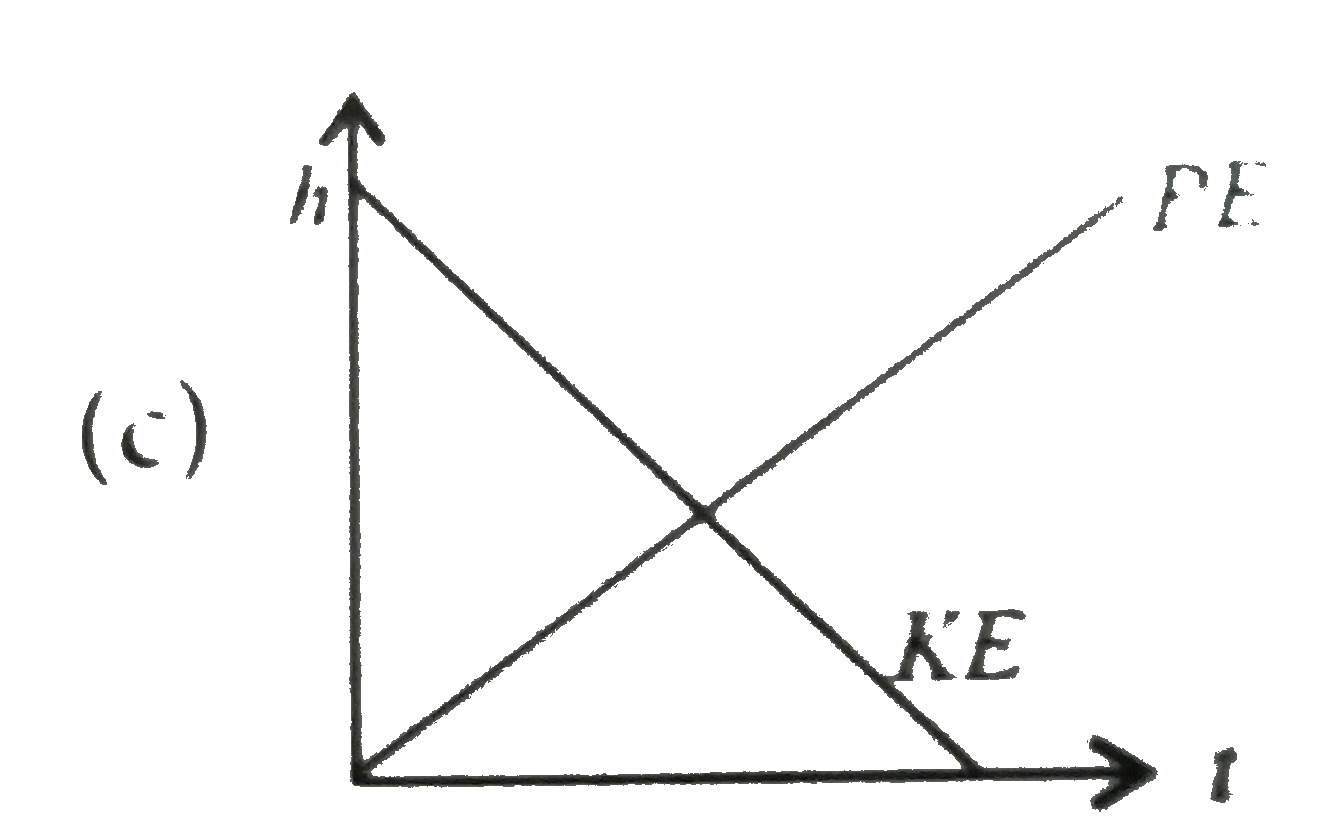 D
D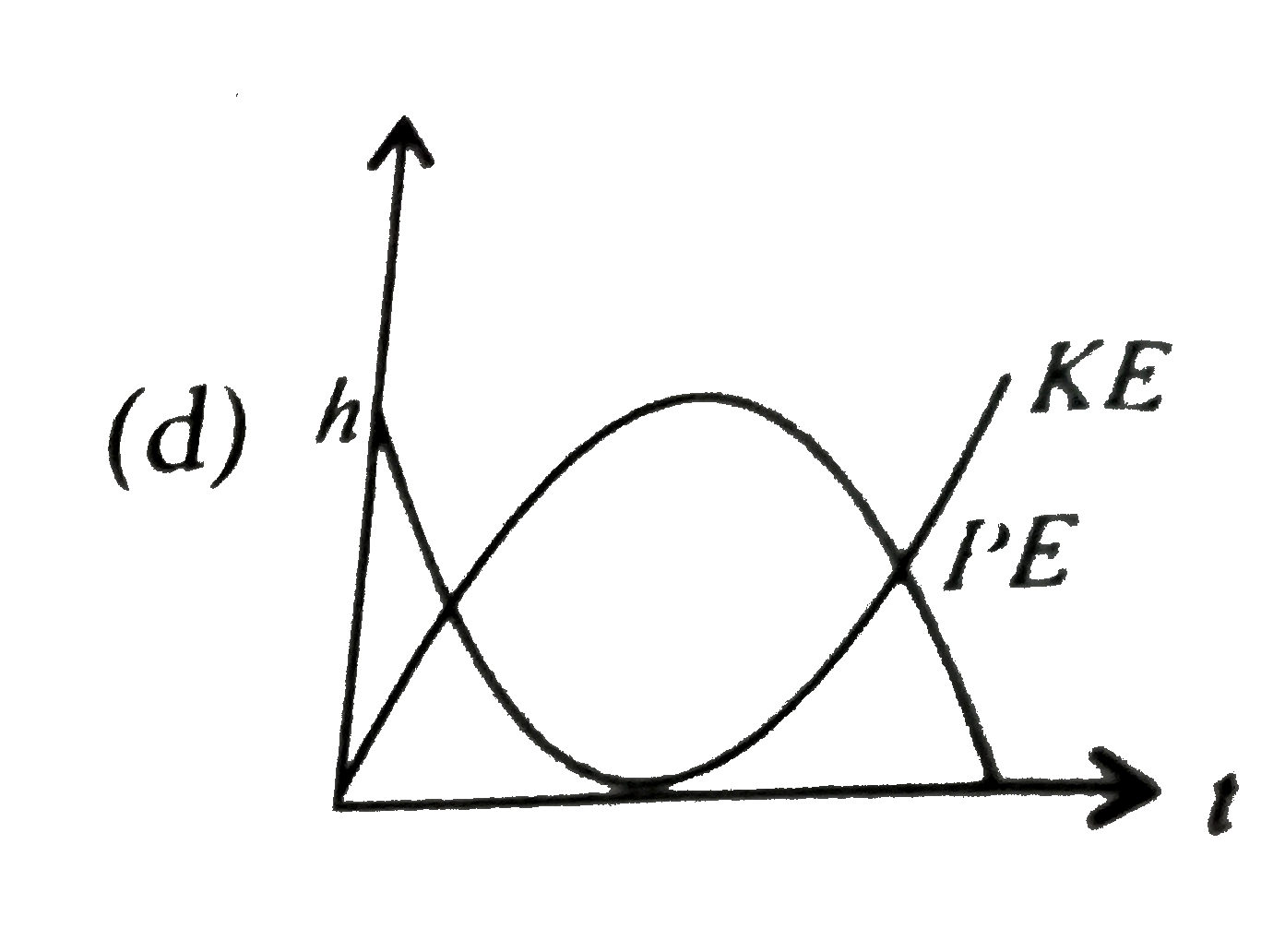
A clamped string is oscillating in nth harmonic, then :-
A. Total energy of oscilations will be n2 times that of fundamental frequency
B. Total energy of oscillations will be (n−1)2 times that of fundamental frequency
C. Average kinetic energy of the string over a complete oscillations is half of that the total energy of the string
D. None of these
View SolutionAt what height from the surface of the earth, the total energy of satellite is equal to its potential energy at a height 2R from the surface of the earth (R=radius of earth)
View SolutionSand is pouring from a pipe at the rate of 12cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always 1/6th of the radius of the base. How fast does the height of the sand cone increase when the height in 4 cm?
View SolutionSand is pouring from a pipe at the rate of 12cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always 1/6th of the radius of the base. How fast does the height of the sand cone increase when the height in 4 cm?
View SolutionA block of mass m is kept on the floor of a freely falling lift .During the free fall of the lift, the block is pulled horizontally with a force of F=5N,μs=0.1The friction force on the block will be
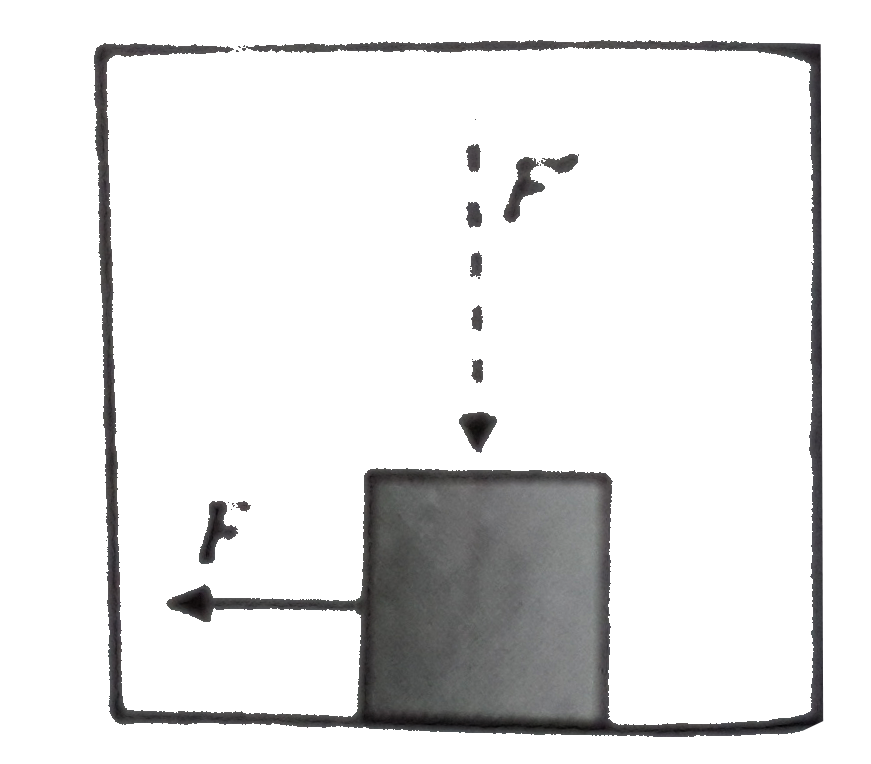
View SolutionAn object of mass 'm' is allowed to fall freely from a point A as shown in the figure.
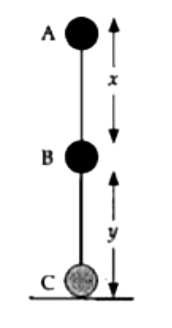
Calculate the total mechanical energy of object at:
Point A
View SolutionIf a stone dropped from the top of a tower travels half, of the height of the tower during last second of its fall, the time of fall is (in seconds)
View Solution
