If A=(3,1,-2) ; B=(-1,0,1) and l,m are projections of AB on y-axis, zx plane respectively, then 3l2−m+1=
0
-1
11
27
Step by step video & image solution for If A=(3,1,-2) ; B=(-1,0,1) and l,m are projections of AB on y-axis, zx plane respectively, then 3l^2-m+1= 0-11127 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
If A=(3,1,-2) ; B=(-1,0,1) and l,m are projections of AB on y-axis, zx plane respectively, then 3l2−m+1=
0
-1
11
27View SolutionConside the matrices A=⎡⎢⎣1234121−11⎤⎥⎦ B=⎡⎢⎣21341−1223⎤⎥⎦ C=⎡⎢⎣14122⎤⎥⎦ D=⎡⎢⎣131114⎤⎥⎦. Now x=⎡⎢⎣xyz⎤⎥⎦is such that solutions of equation AX=C and BX=D represent two points L andM respectively in 3 dimensional space. If L' and M' are hre reflections of L and M in the plane x+y+z=9 then find coordinates of L,M,L',M'
View SolutionConside the matrices A=⎡⎢⎣1234121−11⎤⎥⎦ B=⎡⎢⎣21341−1223⎤⎥⎦ C=⎡⎢⎣14122⎤⎥⎦ D=⎡⎢⎣131114⎤⎥⎦. Now x=⎡⎢⎣xyz⎤⎥⎦is such that solutions of equation AX=C and BX=D represent two points L andM respectively in 3 dimensional space. If L' and M' are hre reflections of L and M in the plane x+y+z=9 then find coordinates of L,M,L',M'
View SolutionIf l1,m1,n1,l2,m2,n2andl3,m3,n3 are direction cosines of three mutuallyy perpendicular lines then, the value of ∣∣ ∣∣l1m1n1l2m2n2l3m3n3∣∣ ∣∣ is
View SolutionIf L=(2±0.01)mandB=(1±0.02)m then L/B is
View SolutionThe moment of inertia of a thin square plate ABCD, fig, of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
where l1,l2,l3andl4 are respectively the moments of intertial about axis 1,2,3 and 4 which are in the plane of the plate.
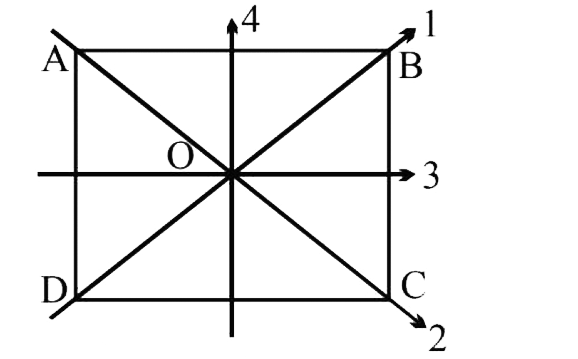 View Solution
View SolutionO is the origin and lines OA, OB and OC have direction cosines lr,mrandnr(r=1,2and3). If lines OA', OB' and OC' bisect angles BOC, COA and AOB, respectively, prove that planes AOA', BOB' and COC' pass through the line xl1+l2+l3=ym1+m2+m3=zn1+n2+n3.
View SolutionA=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ and B=⎡⎢⎣p1q1r1p2q2r2p3q3r3⎤⎥⎦
Where pi,qi,ri are the co-factors of the elements li,mi,ni for i=1,2,3. If (l1,m1,n1),(l2,m2,n2) and (l3,m3,n3) are the direction cosines of three mutually perpendicular lines then (p1,q1,r1),(p2,q2,r2) and (p3,q,r3) areView SolutionStatement-I (S1): If A(x1,y1),B(x2,y2),C(x3,y3) are non-collinear points. Then, every point (x, y) in the plane of △ABC, can be expressed in the form (kx1+lx2+mx3k+l+m,ky1+ly2+my3k+l+m)
Statement-II (S2) The condition for coplanarity of four A(a), B(b), C(c), D(d) is that there exists scalars l, m, n, p not all zeros such that la+mb+nc+pd=0 where l+m+n+p=0.View SolutionIf (l1,m1,n1),(l2,m2,n2) are D.C's of two lines, then (l1m2−l2m1)2+(m1n2−n1m2)2+(n1l2−n2l1)2+(l1l2+m1m2+n1n2)2=
View Solution
