For the given pair of equations, two statements are given below - one labelled Assertion (A) and the other labelled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
2x+5y=15
3x+6y=7
Assertion (A): The given pair of equations can be reduced to a pair of linear equations in two variables
Reason (R): In the given equations, y can be substituted by 1p
Both (A) and (R) are true and (R) is correct explanation of the (A).
Both (A) and (R) are true but (R) is not the correct explanation of the (A).
(A) is true but (R) is false.
(A) is false but (R) is true.
The correct Answer is:B
To solve the problem, we need to analyze the given equations and the statements made in the assertion and reason.
Given Equations:
1. 2x+5y=15
2. 3x+6y=7
Step 1: Rewrite the Equations
To analyze these equations, we can introduce a new variable for 1x. Let's denote:
p=1x
Then we can rewrite the equations in terms of p.
Step 2: Substitute p into the Equations
Now, substituting p into the equations:
1. The first equation becomes:
2p+5y=15
2. The second equation becomes:
3p+6y=7
Step 3: Analyze the New Equations
Now we have a new pair of equations:
1. 2p+5y=15
2. 3p+6y=7
These equations are now linear in terms of the variables p and y.
Step 4: Check the Assertion and Reason
- Assertion (A): The given pair of equations can be reduced to a pair of linear equations in two variables.
- This is True because we have successfully rewritten the equations in terms of p and y, which are linear.
- Reason (R): In the given equations, y can be substituted by 1p.
- This is False because the substitution of y as 1p does not directly relate to the original equations. The equations are already linear in p and y without needing to express y in terms of p.
Conclusion
The correct option that describes the statements is:
- Assertion (A) is True.
- Reason (R) is False.
1. 2x+5y=15
2. 3x+6y=7
To analyze these equations, we can introduce a new variable for 1x. Let's denote:
p=1x
Then we can rewrite the equations in terms of p.
Now, substituting p into the equations:
1. The first equation becomes:
2p+5y=15
2. The second equation becomes:
3p+6y=7
Now we have a new pair of equations:
1. 2p+5y=15
2. 3p+6y=7
- Assertion (A): The given pair of equations can be reduced to a pair of linear equations in two variables.
- This is True because we have successfully rewritten the equations in terms of p and y, which are linear.
- This is False because the substitution of y as 1p does not directly relate to the original equations. The equations are already linear in p and y without needing to express y in terms of p.
The correct option that describes the statements is:
- Assertion (A) is True.
- Reason (R) is False.
Topper's Solved these Questions
- BOOK - CBSE MODEL PAPERCHAPTER - PRACTICE PAPER 2022EXERCISE - Multiple Choice Questions60videos
PRACTICE PAPER 2022
- BOOK - CBSE MODEL PAPERCHAPTER - CASE STUDY QUESTIONS CLASS 10TH EXAM 2020-21EXERCISE - MCQs239videos
CASE STUDY QUESTIONS CLASS 10TH EXAM 2020-21
- BOOK - CBSE MODEL PAPERCHAPTER - QUESTION BANK 2021EXERCISE - QUESTIONS60videos
QUESTION BANK 2021
Similar Questions
Some reactions require conditions like specific temperature, pressure, etc. While writing chemical equations for such reactions, where are these conditions usually mentioned?
02:14View SolutionMahesh works as a manager in a hotel. He has to arrange seats in hall for a function. A hall has a certain number of chairs. Guests want to sit in different groups like in pairs, triplets, quadruplets, fives and sixes etc. When Mahesh arranges chairs in such pattern like in 2’s, 3’s, 4’s 5’s and 6’s then 1, 2, 3, 4 and 5 chairs are left respectively. But when he arranges in 11’s, no chair will be left.

In the hall, how many chairs are available?02:34View SolutionA biogas plant is where biogas is produced by fermenting biomass
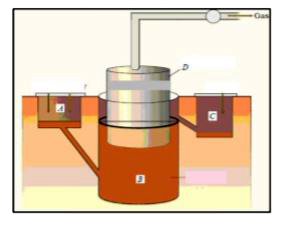
In which of the parts would you find anaerobic bacteria ?01:57View SolutionIn each of the following two questions two statements are given one labelled as the Assertion(A) or Statement I and the other labelled as the reason (R) or statement II. Examine these statements carefully and mark the correct choice as per following instructions
Assertion (A) - The standard unit for expressing the mass of an atom is a.m.u.
Reason (R) - a.m.u. is also called avogram03:24View SolutionGiven below are two statements : one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A : Hydrogen is the most abundatn element in the Universe, but it is not the most abundant gas in the troposphere .
Reason R : Hydrogen is the lightest element . In the light of the above statements , choose the correct answer from the options given below :02:33View SolutionSTATEMENT - 1 : When a rod lying freely is heated, no thermal stress is developed in it.
and
STATEMENT - 2 : On heating, the length of the rod increase.05:06View SolutionGiven below are two statement : one is labelled as Assertion A and the other is labelled as Reason R: Assertion A: Size of Np^( 3 +) ion is greater than Bk^(3 + ) ion. Reason R: The above is a consequence of the lanthanoid contraction. In the light of the above statements, choose the correct answer from the options given below :
04:22View SolutionGiven below are two statements : one is labelled as Assertion A and the other is labelled as Reason R: Assertion A: The H-O-H bond angle in water molecule is 104.5^(@) Reason R: The lone pair - lone pair repulsion of electrons is higher than the bond pair - bond pair repulsion. In the light of the above statements, choose the correct answer from the options given below:
02:07View SolutionGiven below are two statements, one is labelled as Assertion (A) and other is labelled as Reason (R).
Assertion (R) : Gabriel phthalimide synthesis cannot be used to prepare aromatic primary amines.
Reason : Aryl halides do not undergo nucleophilic substitution reaction. In the light of the above statements, choose the correct answer from the options given below03:00View SolutionGiven below are two statements : One is labelled as Assertion A and the other labelled as Reason R.
Assertion A : Lithium halides are some what covalent in nature.
Reason R : Lithium possess high polarisation capability.
In the light of the above statements, choose the most appropriate answer from the options given below :02:37View SolutionGiven below are two statements labelled as Assertion (A) and Reason (R) Assertion(A): Molarity of a solution changes with temperature. Reason (R): Molarity is a colligative property. Select the most appropriate answer from the options given below:
03:42View SolutionGiven below are two statements labelled as Assertion (A) and Reason (R) Assertion (A):Cryoscopic constant depends on nature of solvent. Reason(R):Cryoscopic constant is a universal constant. Select the most appropriate answer from the options given below:
03:33View SolutionGiven below are two statements : one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : Photochemical smog causes cracking of rubber.
Reason (R) : Presence of ozone, nitric oxide, acrolein, formaldehyde and peroxyacetyl nitrate in photochemical smog makes it oxidizing.
Choose the most appropriate answer from the options given below :02:39View SolutionGiven below are two statements: one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : Heavy water is used for the study of reaction mechanism.
Reason (R) : The rate of reaction for the cleavage of O - H bond is slower than that of O - D bond.
Choose the most appropriate answer from the options given below :02:09View SolutionGiven below are two statements: one is labelled as Assertion (A) and the other is labelled as Reason (R). Assertion (A) : Barium carbonate is insoluble in water and is highly stable. Reason (R) : The thermal stability of the carbonates increases with increasing cationic size. Choose the most appropriate answer from the options given below :
View SolutionGiven below are two statements: one is labelled as Assertion (A) and the other is labelled as Reason (R). Assertion (A) : Sucrose is a disaccharide and a non-reducing sugar. Reason (R) : Sucrose involves glycosidic linkage between C_1 of D-glucose and C_2 of a-fructose. Choose the most appropriate answer from the options given below :
01:57View Solution

