Give the polynomial of degree 2 with sum and product of its zeros as −12 and -3 respectively:
(x2−x+6)=0
(2x2+x−6)=0
(x2+x−3)=0
(x2−2x+3)=0
The correct Answer is:B
To find a polynomial of degree 2 with the given sum and product of its zeros, we can use the standard form of a quadratic polynomial, which is:
P(x)=x2−(sumofzeros)⋅x+(productofzeros)
Step 1: Identify the sum and product of the zeros
We are given:
- Sum of the zeros S=−12
- Product of the zeros P=−3
Step 2: Substitute the values into the polynomial formula
Using the formula for the polynomial, we substitute the values of the sum and product:
P(x)=x2−(−12)x+(−3)
Step 3: Simplify the polynomial
Now we simplify the expression:
P(x)=x2+12x−3
Step 4: Clear the fraction (optional)
To eliminate the fraction, we can multiply the entire polynomial by 2:
P(x)=2(x2+12x−3)
P(x)=2x2+x−6
Final Polynomial
Thus, the polynomial of degree 2 is:
P(x)=2x2+x−6
We are given:
- Sum of the zeros S=−12
- Product of the zeros P=−3
Using the formula for the polynomial, we substitute the values of the sum and product:
Now we simplify the expression:
To eliminate the fraction, we can multiply the entire polynomial by 2:
P(x)=2x2+x−6
Thus, the polynomial of degree 2 is:
Topper's Solved these Questions
Similar Questions
Case Study-2:
Radha decorated the door of her house with garlands on the occassion of Diwali. Each garland forms the shape of a parabola as shown in the figure.
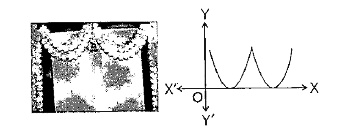
A quadratic polynomial with the sum and product of its zeroes as 1 and -2 respectively, is:
View SolutionRadha decorated the door of her house with garlands on the occassion of Diwali. Each garland forms the shape of a parabola.
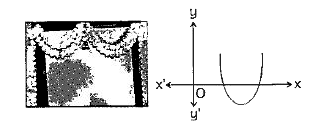
A quadratic polynomial with the sum and product of its zeroes as -1 and -2 respectively, is:
View SolutionFind the polynomial whose sum and product of the zeros are −12 and 12 respectively.
View SolutionFind a quadratic polynomial, the sum and product of whose zeroes are - 3 and 2 respectively.
View SolutionFind the quadratic polynomial, the sum and product of whose zeroes are - 3 and 2 respectively. Hence find the zeroes.
View SolutionFind a quadratic polynomial, the sum and product of whose zeros are −5and6 respectively.
View SolutionFind a quadratic polynomial, the sum and product of whose zeroes are −3and 2, respectively.
View SolutionFind a quadratic polynomial, the sum and product of whose zeros is 4 and 1 respectively.
View SolutionFind the quadratic polynomial sum and product of whose zeroes are -1 and -20 respectively. Also, find the zeroes of the polynomial so obtained
View SolutionFrom a quadratic polynomial, the sum and product of whose zeros are (−3) and 2 respectivily.
View Solution
