A quadratic polynomial having sum and product of its zeroes as 5 and 0 respectively is
x2+5x
2x(x−5)
5x2−1
x2−5x+5
To find the quadratic polynomial with the given sum and product of its zeroes, we can use the standard form of a quadratic polynomial based on its roots.
1. Identify the sum and product of the zeroes:
- Given: Sum of the zeroes (α + β) = 5
- Given: Product of the zeroes (α * β) = 0
2. Use the standard form of a quadratic polynomial:
- The standard form of a quadratic polynomial based on its roots is:
f(x)=x2−(sum of zeroes)⋅x+(product of zeroes)
3. Substitute the values into the polynomial:
- Substitute the sum and product into the polynomial:
f(x)=x2−(5)x+(0)
4. Simplify the polynomial:
- This simplifies to:
f(x)=x2−5x
5. Final polynomial:
- Therefore, the quadratic polynomial is:
f(x)=x2−5x
- Given: Sum of the zeroes (α + β) = 5
- Given: Product of the zeroes (α * β) = 0
- The standard form of a quadratic polynomial based on its roots is:
f(x)=x2−(sum of zeroes)⋅x+(product of zeroes)
- Substitute the sum and product into the polynomial:
f(x)=x2−(5)x+(0)
- This simplifies to:
f(x)=x2−5x
- Therefore, the quadratic polynomial is:
f(x)=x2−5x
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 1 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 BASICEXERCISE - SECTION-B
20 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 BASICEXERCISE - SECTION-C (CASE STUDY)
10 Videos
- CBSE BOARDS 2020BOOK - X BOARDSCHAPTER - CBSE BOARDS 2020EXERCISE - QUESTION
42 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 STANDARDBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 STANDARDEXERCISE - SECTION-C (CASE STUDY)
10 Videos
Similar Questions
Case Study-2:
Radha decorated the door of her house with garlands on the occassion of Diwali. Each garland forms the shape of a parabola as shown in the figure.
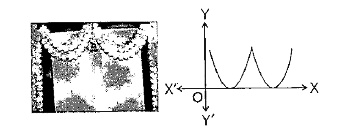
A quadratic polynomial with the sum and product of its zeroes as 1 and -2 respectively, is:
View SolutionRadha decorated the door of her house with garlands on the occassion of Diwali. Each garland forms the shape of a parabola.
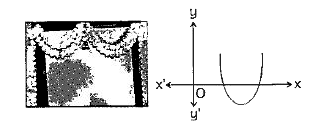
A quadratic polynomial with the sum and product of its zeroes as -1 and -2 respectively, is:
View SolutionFind a quadratic polynomial, the sum and product of whose zeros are −5and6 respectively.
View SolutionFind a quadratic polynomial, the sum and product of whose zeros is 4 and 1 respectively.
View SolutionFind the quadratic polynomial sum and product of whose zeroes are -1 and -20 respectively. Also, find the zeroes of the polynomial so obtained
View SolutionFind a quadratic polynomial, the sum and product of whose zeroes are - 3 and 2 respectively.
View SolutionFind a quadratic polynomial, the sum and product of whose zeroes are −3and 2, respectively.
View SolutionFind the quadratic polynomial, the sum and product of whose zeroes are - 3 and 2 respectively. Hence find the zeroes.
View SolutionFind a quadratic polynomial, sum and product of whose zeroes −3and2 respectively.
View SolutionFrom a quadratic polynomial, the sum and product of whose zeros are (−3) and 2 respectivily.
View Solution
