It is given that ΔDEF~ΔPQR.EF:QR=3:2, then value of ar(DEF) : ar(PQR) is
4:9
4:8
9:2
9:4
To solve the problem, we need to find the ratio of the areas of triangles DEF and PQR given that they are similar and the ratio of one pair of corresponding sides is provided.
1. Understanding Similar Triangles:
Since triangles DEF and PQR are similar (denoted as ΔDEF ~ ΔPQR), we know that the ratios of their corresponding sides are equal.
2. Given Ratio of Sides:
We are given the ratio of the sides EF and QR as 3:2. This can be expressed as:
EFQR=32
3. Using the Area Ratio Theorem:
The theorem states that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
ar(DEF)ar(PQR)=(EFQR)2
4. Substituting the Given Ratio:
Now, we substitute the given ratio of EF to QR into the equation:
ar(DEF)ar(PQR)=(32)2
5. Calculating the Square:
Calculate the square of the ratio:
(32)2=94
6. Final Ratio of Areas:
Thus, we have:
ar(DEF)ar(PQR)=94
Conclusion:
The ratio of the areas of triangles DEF and PQR is:
ar(DEF):ar(PQR)=9:4
Since triangles DEF and PQR are similar (denoted as ΔDEF ~ ΔPQR), we know that the ratios of their corresponding sides are equal.
We are given the ratio of the sides EF and QR as 3:2. This can be expressed as:
EFQR=32
The theorem states that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
ar(DEF)ar(PQR)=(EFQR)2
Now, we substitute the given ratio of EF to QR into the equation:
ar(DEF)ar(PQR)=(32)2
Calculate the square of the ratio:
(32)2=94
Thus, we have:
ar(DEF)ar(PQR)=94
The ratio of the areas of triangles DEF and PQR is:
ar(DEF):ar(PQR)=9:4
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 1 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 BASICEXERCISE - SECTION-B
20 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 BASICEXERCISE - SECTION-C (CASE STUDY)
10 Videos
- CBSE BOARDS 2020BOOK - X BOARDSCHAPTER - CBSE BOARDS 2020EXERCISE - QUESTION
42 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 STANDARDBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 STANDARDEXERCISE - SECTION-C (CASE STUDY)
10 Videos
Similar Questions
Knowledge Check
It is given that ΔABC−ΔPQR, with BCQR=14. Then arΔPQRarΔABC is equal to:
A16B3C13D19It is given that ΔABC~ΔPRQandBCQR=23 then ar(ΔPQR)ar(ΔABC)=?
A23B32C49D94In ΔDEFandΔPQR, if PQ =DE, EF=PR and FD =QR, then
AΔDEF≡ΔRPQBΔDEF≡ΔQPRCΔDEF≡ΔQRPDΔDEF≡ΔPQR
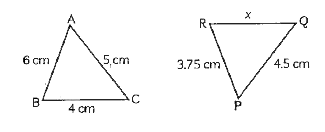
Given that △PQR is similar to △BAR, find the value of x:
View SolutionIn ΔDEFandΔPQR, if PQ =DE, EF=PR and FD =QR, then
View SolutionIn ΔDEFandΔPQR, if PQ = DE , EF = PR and FD = QR , then
View SolutionIn ΔABC, it is given that AB=9cm,BC=6cm,andCA=7.5cm. AlsoΔDEF is givne such that EF=8cmandΔDEF~ΔABC. Then perimeter of ΔDEF is
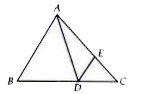
View SolutionIn the given figure, AD is the median and E is any point on AC, such that ar(ΔMDE) : ar(ΔABD) = 2 : 3, then find the ratio of ar(ΔEDC): ar(ΔABC).
View Solution