A circle of radius 3 units is centered at (0,0) . Which of the following points lie outside the circle ?
(-1,-1)
(0,3)
(1,2)
(3,1)
To determine which points lie outside the circle centered at (0,0) with a radius of 3 units, we can follow these steps:
1. Identify the Circle's Equation:
The equation of a circle centered at (h, k) with radius r is given by:
(x−h)2+(y−k)2=r2
For our circle, h = 0, k = 0, and r = 3. Thus, the equation becomes:
x2+y2=32
Simplifying gives:
x2+y2=9
2. Determine the Condition for Points:
A point (x, y) lies outside the circle if:
x2+y2>9
It lies on the circle if:
x2+y2=9
And it lies inside the circle if:
x2+y2<9
3. Evaluate Each Point:
We will check each point against the condition x2+y2>9.
- Point A: (1, 1)
12+12=1+1=2(inside the circle)
- Point B: (0, 3)
02+32=0+9=9(on the circle)
- Point C: (1, 2)
12+22=1+4=5(inside the circle)
- Point D: (3, 1)
32+12=9+1=10(outside the circle)
4. Conclusion:
The only point that lies outside the circle is Point D: (3, 1).
Final Answer:
The point that lies outside the circle is (3, 1).
The equation of a circle centered at (h, k) with radius r is given by:
(x−h)2+(y−k)2=r2
For our circle, h = 0, k = 0, and r = 3. Thus, the equation becomes:
x2+y2=32
Simplifying gives:
x2+y2=9
A point (x, y) lies outside the circle if:
x2+y2>9
It lies on the circle if:
x2+y2=9
And it lies inside the circle if:
x2+y2<9
We will check each point against the condition x2+y2>9.
12+12=1+1=2(inside the circle)
02+32=0+9=9(on the circle)
12+22=1+4=5(inside the circle)
32+12=9+1=10(outside the circle)
The only point that lies outside the circle is Point D: (3, 1).
The point that lies outside the circle is (3, 1).
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 1 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 BASICEXERCISE - SECTION-C (CASE STUDY)
10 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 BASICEXERCISE - SECTION-C (CASE STUDY)
10 Videos
- CBSE BOARDS 2020BOOK - X BOARDSCHAPTER - CBSE BOARDS 2020EXERCISE - QUESTION
42 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 STANDARDBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 STANDARDEXERCISE - SECTION-C (CASE STUDY)
10 Videos
Similar Questions
One circle has a radius of 5 and its centre at (0,5). A second circle has a radius of 12and its centre at (12,0). What is the length of a radius of a third circle which passes through the centre of the second circle and both the points of intersection of the first two circles.
View SolutionTangents from a Point Outside the circle.
View Solution
Knowledge Check
Two points (1,1) and (1,5) lie on the circumference of a circle. Which of the following can be the area of that circle ?
A2√2πB4πC3√3πD6.67πSuppose Q is a point on the circle with center P and radius 1, as shown in the figure , R is a point outside the circle such that QR=1and∠QRP=2∘ . Let S be the point where the segment RP intersects the given circle. Then measure of ∠RQS equals-
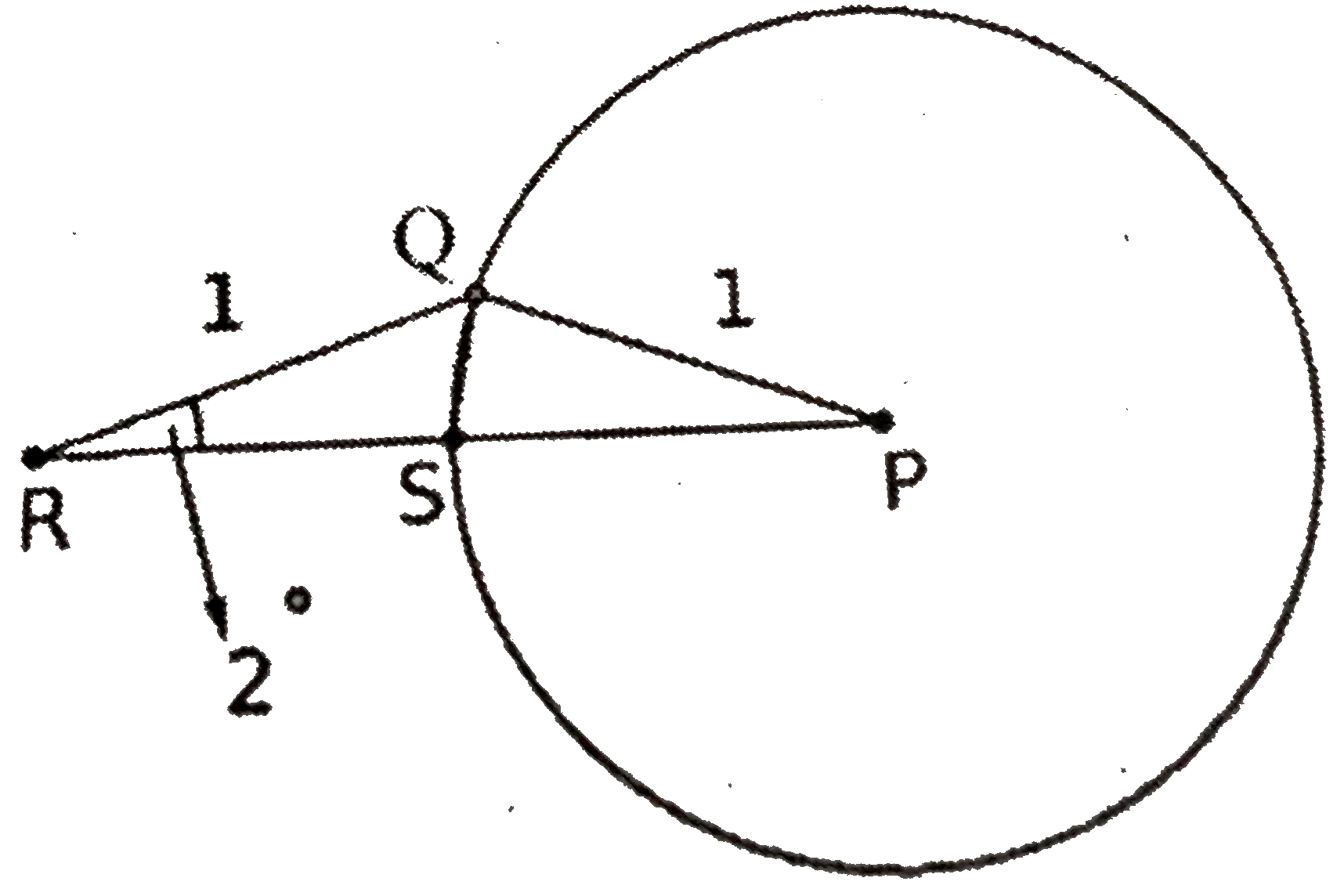 A86∘B87∘C88∘D89∘
A86∘B87∘C88∘D89∘
A circle touches the y-axis at the point (0, 4) and passes through the point ( 2, 0). Which of the following lines is not a tangent to the circle ?
View SolutionA circle of radius 2 has its centre at (2, 0) and another circle of radius 1 has its centre at (5, 0). A line is tangent to the two circles at point in the first quadrant. The y-intercept of the tangent line is
View SolutionWhat is the equation of the circle in complex plane with radius 2 and centre at 1+i. Does the origin lie within this circle, on the circle or outside it? Does any real number lie on this circle?
View SolutionA square is inscribed in a circle with radius 7√2 units. Find the probability that a point lying inside the circle selected at random will lie inside the square.
View SolutionA circle has its centre at the origin and a point P (5,0) lies on it . The point Q (6,8) lies outside the circle.
View SolutionA tangent is drawn from an external point O to a circle of radius 3 units at P such that OP = 4 units. If C is the centre of the circle, then the sine of the angle COP is
View Solution
