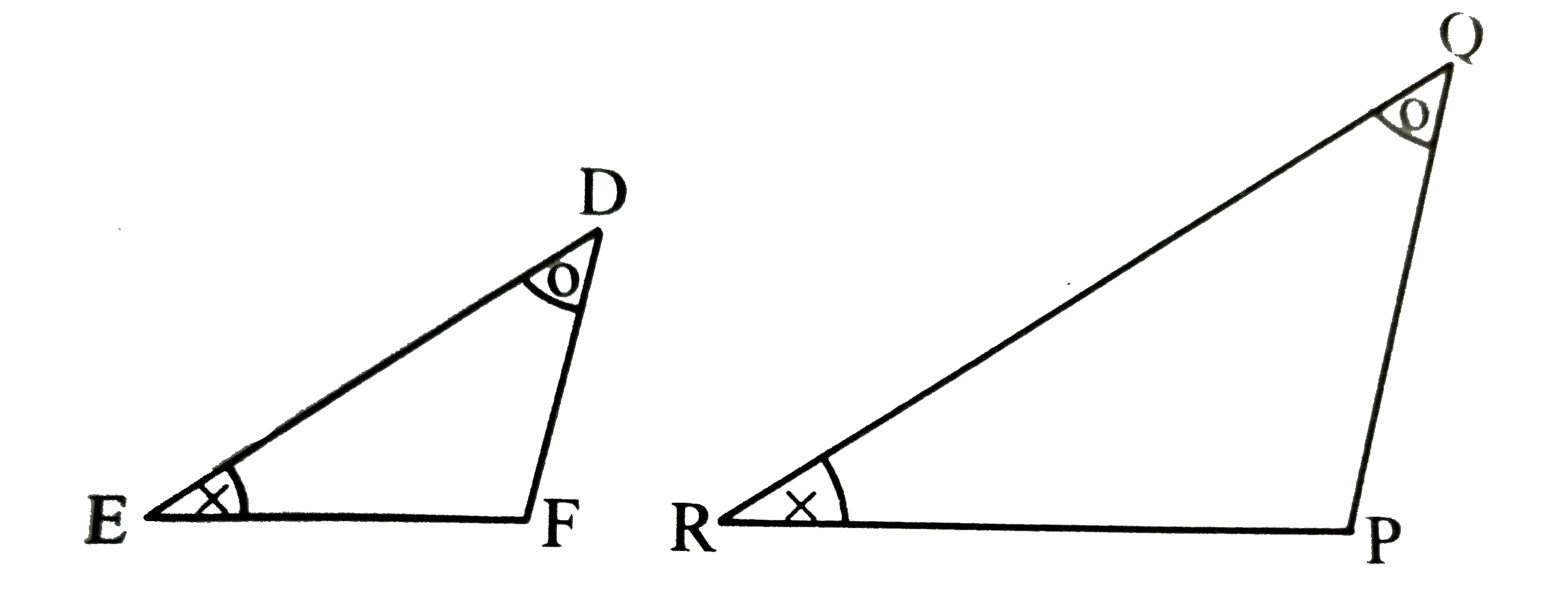
If in two Δs DEF and PQR, ∠D=∠Q and ∠R=∠E, then which of the following is not true?
EFPR=DFPQ
DEPQ=EFRP
DEQR=DFPQ
EFRP=DEQR
To solve the problem, we need to analyze the given information about triangles DEF and PQR, where angle D = angle Q and angle R = angle E. We want to determine which of the statements regarding these triangles is not true.
1. Identify the Given Angles:
We have:
- Angle D = Angle Q
- Angle R = Angle E
2. Apply the Angle-Angle (AA) Similarity Criterion:
Since we have two pairs of equal angles, we can conclude that triangles DEF and PQR are similar by the Angle-Angle (AA) similarity criterion. This means:
- Triangle DEF ~ Triangle PQR
3. Corresponding Angles:
From the similarity of triangles, we know that the corresponding angles are equal. Therefore:
- Angle F = Angle P (since they are the third angles in both triangles)
4. Set Up the Proportionality of Sides:
The sides of similar triangles are proportional. Thus, we can write:
DEQR=EFRP=DFPQ
5. Evaluate the Statements:
We need to check the given statements to find out which one is not true based on the proportionality established above.
- Statement A: EFPR=DFPQ (True)
- Statement B: DEPQ=EFRB (Not True)
- Statement C: DEQR=DFPQ (True)
- Statement D: EFRP=DEQR (True)
6. Conclusion:
The statement that is not true is DEPQ=EFRB.
Final Answer:
The statement that is not true is: DEPQ=EFRB.
We have:
- Angle D = Angle Q
- Angle R = Angle E
Since we have two pairs of equal angles, we can conclude that triangles DEF and PQR are similar by the Angle-Angle (AA) similarity criterion. This means:
- Triangle DEF ~ Triangle PQR
From the similarity of triangles, we know that the corresponding angles are equal. Therefore:
- Angle F = Angle P (since they are the third angles in both triangles)
The sides of similar triangles are proportional. Thus, we can write:
DEQR=EFRP=DFPQ
We need to check the given statements to find out which one is not true based on the proportionality established above.
- Statement B: DEPQ=EFRB (Not True)
- Statement C: DEQR=DFPQ (True)
- Statement D: EFRP=DEQR (True)
The statement that is not true is DEPQ=EFRB.
The statement that is not true is: DEPQ=EFRB.
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 2 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2 BASICEXERCISE - SECTION B
20 Videos
- QUESTION PAPER 2022 TERM 1 SET 2 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2 BASICEXERCISE - SECTION C (Case Study Based Question)
10 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 STANDARDBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 STANDARDEXERCISE - SECTION-C (CASE STUDY)
10 Videos
- QUESTION PAPER 2022 TERM 1 SET 2 STANDARDBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2 STANDARDEXERCISE - SECTION-C
10 Videos
Similar Questions
Knowledge Check
In ΔDEFandΔPQR, it is given that ∠D=∠Qand∠R=∠E, then which of the following is not true?
AEFPR=DFPQBDEPQ=EFRPCDEQR=DFPQDEFRP=DEQRIn an acute angled triangle which one of the following is true
AasecA+bsecB+csecCtanA.tanB.tanC=2RBcosA√4R2−a2=cosB√4R2−b2=cosC√4R2−c2Cb2=a2cos2C+c2cos2A+2accosA.cosCDrcotA2+a=rcotB2+b=rcotC2+cIn ΔABCandΔPQR , If AB=AC, ∠C=∠P and ∠B=∠Q, then the two triangles are
Aisosceles but not congruentBisosceles and congruentCcongruent but not isoscelesDNeither congruent nor isosceles
If for ΔABCandΔDEF , the correspondence CAB↔EDF gives a congruence then which of the following is not true ?
View SolutionIf for ΔABC and <DEF the correspondence CAB↔EDF gives a congruence, then which of the following is not true?
View SolutionIf ΔABC~ΔEDFandΔABC is not similar to ΔDEF then which of the following is not ture ?
View SolutionIn a right angled triangle aBC with ∠A=90∘, which of the following results are true ?
View SolutionIn △ABCand△DEF , if ∠A=∠F,∠B=∠D and AB = FD , then which one of the folloing congruence conditions applies :
View Solution