The reflective surface is given by y = 2 sin x. The reflective surface is facing positive axis. What is the least value of coordinates of the point where a ray parallel to positive x-axis becomes parallel to positive y-axis after reflection ?
(π3,√3)
(π2,√2)
(π3,√2)
(π4,√3)
The correct Answer is:A
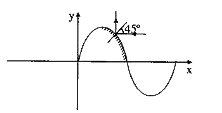
slope of curve dydx=2cosx=1
cosx=12
x=π3
∴y=2sin(π/3)=2√32=√3
Topper's Solved these Questions
Similar Questions
Knowledge Check
The reflective surface is given by y=2sinx. The reflective surface is facing positive axis. What is the least value of coordinate of the point where a ray parallel to positive x-axis becomes parallel to positive y -axis after reflection?
A(π3,√3)B(π2,√2)C(π3,√2)D(π4,√3)The coordinates of images of the point (2,3) when reflected on the y-axis are
A(2,3)B(2,-3)C(-2,-3)D(-2,3)A ray of light is incident on a concave mirror. If it is parallel to the principal axis, the reflected ray will
Apass through the focusBpass through the centre of curvatureCpass through the poleDretrace its path
The point (1,−2) is reflected in the x-axis and then translated parallel to the positive direction of x-axis through a distance of 3 units, find the coordinates of the point in the new position.
View SolutionIF incident ray from point (-1,2) parallel to the axis of the parabola y2=4x strikes the parabola, find the equation of the reflected ray.
View SolutionIf C is the reflection of A(2,4) in x-axis and B is the reflection of C in y-axis then |AB| is 4√k then k=
View SolutionThe point (1,−2) is reflected in the x-axis and then translated parallel to the positive direction of x-axis through a distance of 3 units, find the coordinates of the point in the new position.
View SolutionA ray of light coming from origin after reflectiion at the point P(x,y) of any curve becomes parallel to x-axis, the , equation of the curve may be :
View Solution