A concave mirror of focal length 'f1 ' is placed at a distance of 'd' from a convex lens of focal length 'f2 '. A beam of light coming from infinity and falling on this convex lens-concave mirror combination returns to infinity. The distance d' must equal -
f1+f2
−f1+f2
2f1+f2
−2f1+f2
The correct Answer is:C
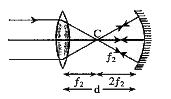
d=f2+2f1
Topper's Solved these Questions
Similar Questions
Knowledge Check
A concave mirrorr of focal length f1 is placed at a distance of d from a convex lens of focal length f2. A beam of light coming from infinity and falling on this convex lens-concave mirrorr combination returns to infinity. The distance d must equal.
A−2f1+f2Bf1+f2C−f1+f2D2f1+f2A concave mirrorr of focal length f1 is placed at a distance of d from a convex lens of focal length f2. A beam of light coming from infinity and falling on this convex lens-concave mirrorr combination returns to infinity. The distance d must equal.
Af1+f2B−f1+f2C2f1+f2D−2f1+f2A concave lens of focal length 20 cm placed in contact with ah plane mirror acts as a convex mirror of focal length
A10 cmB40 cmC60 cmD20 cm
A convex lens of focal length 10 cm is placed in contact with a concave lens of focal length 20 cm. The focal length of this combination of lenses will be:
View SolutionA convex lens of focal length 20 cm is placed in contact with a concave lens of focal length 10 cm. What is the focal length and power of the combination ?
View SolutionAn object is placed at a distance f in the front of a convex mirror. If focal length of the mirror is f, then distance of image from pole of the mirror is
View SolutionA convex lens of focal length 'f' is placed in contact with a concave lens of the same focal length. The equivalent focal length of the combination is
View SolutionA thin convex lens of focal length 10 cm is placed in contact with a concave lens of same material and of same focal length. The focal length of combination will be
View Solution
