The solution set on the number line of the linear inequation:
2y−6<y+2≤2y,y∈N is



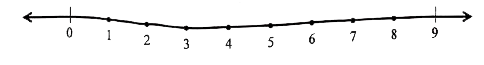
To solve the given linear inequation 2y−6<y+2≤2y where y is a natural number, we will break it down into two parts and solve each part step by step.
Step 1: Solve the first part of the inequation
We start with the first part of the inequation:
2y−6<y+2
Hint: Isolate y by moving terms involving y to one side and constant terms to the other.
1. Subtract y from both sides:
2y−y−6<2
This simplifies to:
y−6<2
2. Add 6 to both sides:
y<2+6
This simplifies to:
y<8
Step 2: Solve the second part of the inequation
Now we solve the second part of the inequation:
y+2≤2y
Hint: Again, isolate y by moving terms involving y to one side.
1. Subtract y from both sides:
y+2−y≤2y−y
This simplifies to:
2≤y
Step 3: Combine the results
Now we have two inequalities:
1. y<8 (from Step 1)
2. y≥2 (from Step 2)
Hint: Combine the inequalities to find the range of y.
This means:
2≤y<8
Step 4: Determine the natural number solutions
Since y must be a natural number (denoted as N), the possible values of y are:
y=2,3,4,5,6,7
Final Answer
The solution set of the inequation on the number line is:
{2,3,4,5,6,7}
We start with the first part of the inequation:
2y−6<y+2
2y−y−6<2
This simplifies to:
y−6<2
y<2+6
This simplifies to:
y<8
Now we solve the second part of the inequation:
y+2≤2y
y+2−y≤2y−y
This simplifies to:
2≤y
Now we have two inequalities:
1. y<8 (from Step 1)
2. y≥2 (from Step 2)
2≤y<8
Since y must be a natural number (denoted as N), the possible values of y are:
y=2,3,4,5,6,7
The solution set of the inequation on the number line is:
{2,3,4,5,6,7}
Topper's Solved these Questions
Similar Questions
Knowledge Check
The following diagram represents the solution of two sets P and Q on the number line:
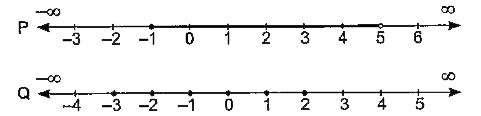
Which of the following inequation has a set Q as its solution?A2x+9≤x+14,x∈WB−11≤3x−2≤4,x∈ZC8−x<4x−2≤6,x∈RD−42<6x+42≤3x+45,x∈ZThe solution set of x in a linear inequation is {−5,−4,−3,−2,−1,0,1,2,}. In set-builder form, it is written as:
A{x:−5≤x≤2,x∈N}B{x:−5≤x≤2,x∈W}C{x:−5≤x≤2,x∈I}D{x:−5≤x≤2,x∈R}In linear inequations, the set, from which the value of the variable x is to be chosen is called the replacement set and its subset, whose elements satisfy given inequation, is called the solution set of the linear inequation. Given A={x:5x−4≥6,x∈R}andB={x:5−x>1,x∈R}.
Answer the following questions:
The solution set of B on the number line is:A B
B C
C D
D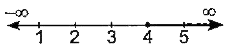
Show that the solution set of the following linear inequations is empty set: x−2y≥0, 2x−y≤−2, x≥0, y≥0
View SolutionShow that the solution set of the following linear inequations is empty set: x+2y, ≤3, 3x+4y≥12, y≥1, x≥0, y≥0
View SolutionSolve the linear inequality |x−2|≥6.
View SolutionIn linear inequations, the set, from which the value of the variable x is to be chosen is called the replacement set and its subset, whose elements satisfy given inequation, is called the solution set of the linear inequation. Given A={x:5x−4≥6,x∈R}andB={x:5−x>1,x∈R}.
Answer the following questions:
The solution set of A on the number line is:
View SolutionIn linear inequations, the set, from which the value of the variable x is to be chosen is called the replacement set and its subset, whose elements satisfy given inequation, is called the solution set of the linear inequation. Given A={x:5x−4≥6,x∈R}andB={x:5−x>1,x∈R}.
Answer the following questions:
On the number line, A∩B is
View Solution