Let be the number of electric field lines going out of an imaginary cube of side a that encloses an isolated point charge 2q and be the corresponding number for an imaginary sphere of radius a that encloses an isolated point charge 3q. Then is:
To solve the problem, we need to determine the ratio of the number of electric field lines going out of two different imaginary shapes enclosing point charges.
1. Understanding Electric Field Lines:
The number of electric field lines emanating from a charge is directly proportional to the magnitude of the charge. This means that if the charge increases, the number of field lines also increases proportionally.
2. Define Variables:
Let N1 be the number of electric field lines going out of a cube enclosing a charge 2q. Let N2 be the number of electric field lines going out of a sphere enclosing a charge 3q.
3. Express N1 and N2:
- Since N1 is proportional to the charge 2q, we can express it as:
N1=k⋅2q
- Similarly, for N2 which is proportional to the charge 3q:
N2=k⋅3q
Here, k is a constant of proportionality that applies to both cases.
4. Calculate the Ratio N1N2:
Now, we can find the ratio of N1 to N2:
N1N2=k⋅2qk⋅3q
- The k and q terms cancel out:
N1N2=23
5. Final Answer:
Thus, the ratio N1N2 is:
N1N2=23
The number of electric field lines emanating from a charge is directly proportional to the magnitude of the charge. This means that if the charge increases, the number of field lines also increases proportionally.
Let N1 be the number of electric field lines going out of a cube enclosing a charge 2q. Let N2 be the number of electric field lines going out of a sphere enclosing a charge 3q.
- Since N1 is proportional to the charge 2q, we can express it as:
N1=k⋅2q
- Similarly, for N2 which is proportional to the charge 3q:
N2=k⋅3q
Here, k is a constant of proportionality that applies to both cases.
Now, we can find the ratio of N1 to N2:
N1N2=k⋅2qk⋅3q
- The k and q terms cancel out:
N1N2=23
Thus, the ratio N1N2 is:
N1N2=23
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 2BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2EXERCISE - SECTION B
24 Videos
- QUESTION PAPER 2022 TERM 1 SET 2BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2EXERCISE - SECTION C
6 Videos
- QUESTION PAPER 2022 TERM 1 SET 1BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1EXERCISE - SECTION-C
6 Videos
- QUESTION PAPER 2023BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2023EXERCISE - Question
43 Videos
Similar Questions
Knowledge Check
If a charge q is placed at the centre of imaginary sphere of radius r then the N.E.I. at a point on such a sphere is
A4πr2qBq4πr2C∈0kEDboth 'b' and 'c'In the adjoining figure, the electric field lines for charges q1andq2 are shown. Identify the sign of the charges.
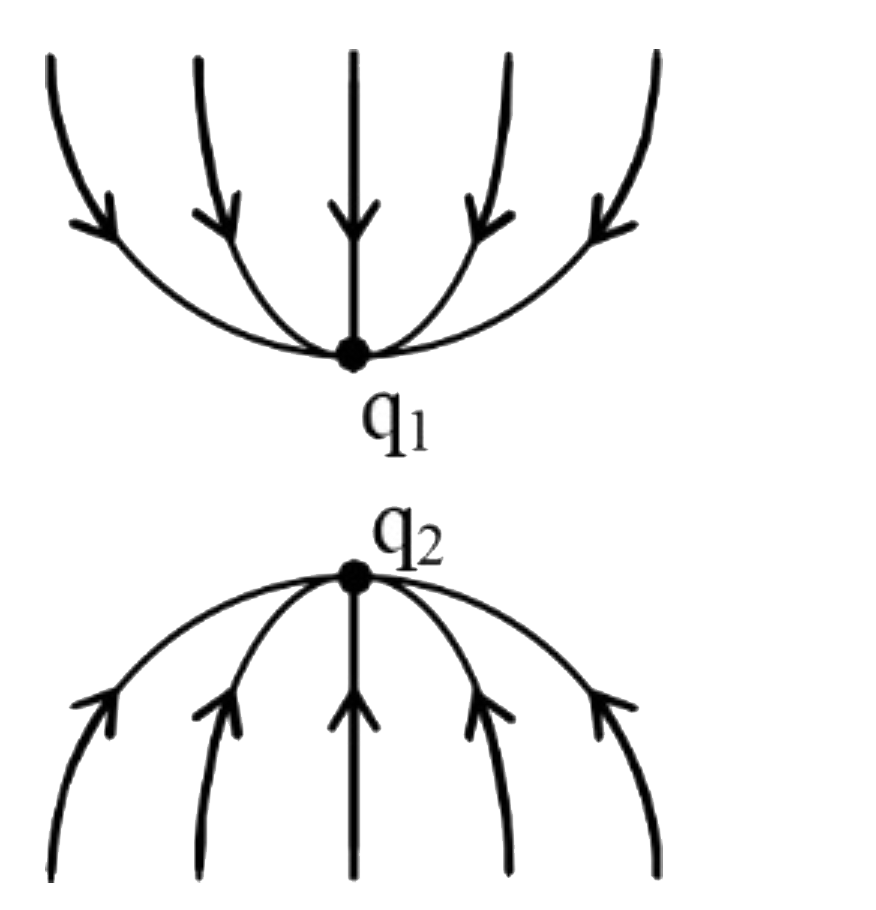 Aboth negativeBupper charge is negatively and lower is positiveCboth positiveDupper charge is positive and lower is negative
Aboth negativeBupper charge is negatively and lower is positiveCboth positiveDupper charge is positive and lower is negativeA sphere of radius R and charge Q is placed inside an imaginary sphere of radius 2R whose centre coincides with the given sphere. The flux related to imaginary sphere is:
AQ∈0BQ2∈0C4Q∈0D2Q∈0
The electric field due to a point charge at a distance R from it is E. If the same charge is placed on a metallic sphere of radius R, the electric field on the surface of the sphere will be nE, then the value of n is
View SolutionIf w be an imaginary cube root of unity, show that 1+wn+w2n=0, for n=2,4.
View SolutionThe number of electric field lines crossing an area ΔSisn1whenΔ→S∣∣→E, while the number of field lines crossing the same area is n2 when Δ→E makes an angles of 30∘ with →E. Then
View SolutionAn electric field line emerges from a positive point charge +q at angle α to the straight line connecting it to a negative point charge −2q as shown in figure. At what angle β with the field line enter the charge−2q ?
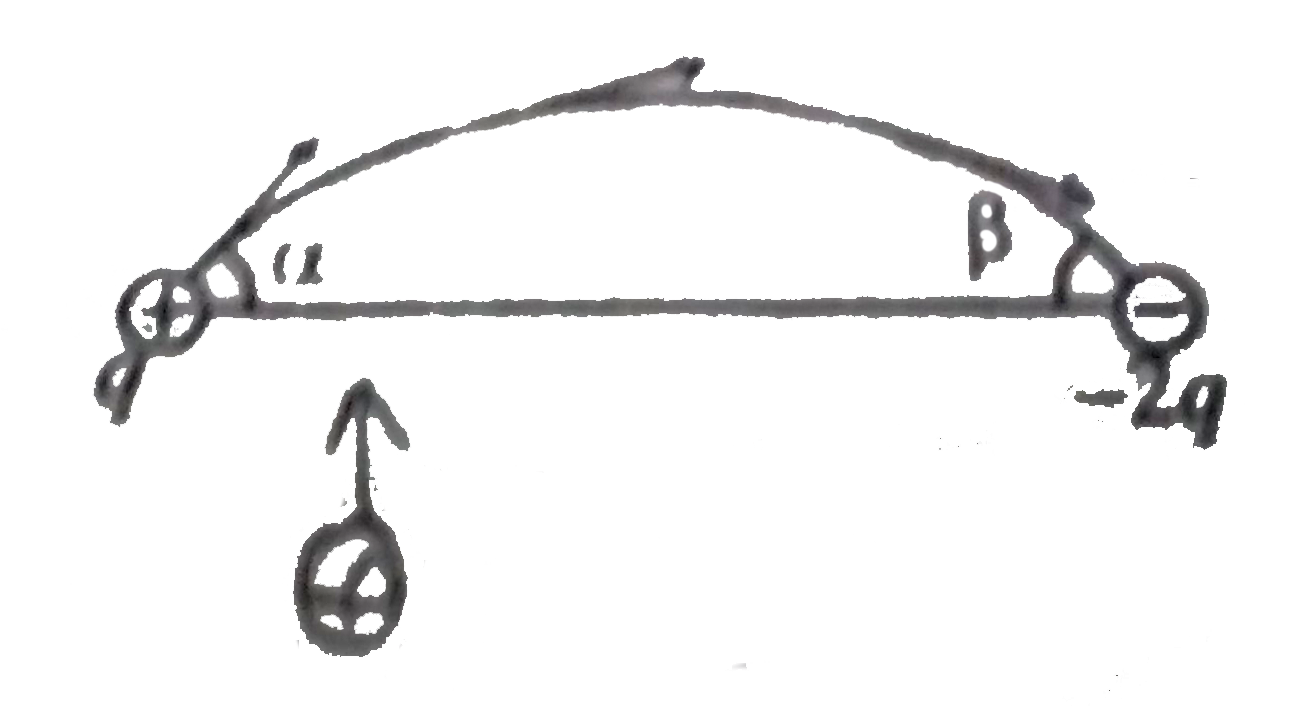
View SolutionA positive point charge Q is bruought mear an isolated metal cube.
View Solution
