A charge Q is located at the centre of a circle of radius r. The work done in moving a test charge q0 from point A to point B (at opposite ends of diameter AB) so as to complete a semicircle is [k=1(4πε0)]:
kq0Qr
kQq0r2
kq0Qr
Zero
To solve the problem of finding the work done in moving a test charge q0 from point A to point B (which are at opposite ends of the diameter of a circle of radius r), we can follow these steps:
1. Understanding the Setup:
- We have a charge Q located at the center of a circle with radius r.
- Points A and B are located at opposite ends of the diameter of the circle.
2. Electric Potential Due to Charge Q:
- The electric potential V at any point in the electric field created by charge Q is given by the formula:
V=kQr
- Here, k=14πϵ0 is the Coulomb's constant.
3. Calculating the Potential at Points A and B:
- Since both points A and B are at the same distance r from the charge Q (as they are at the ends of the diameter), the electric potential at both points is the same:
VA=VB=kQr
4. Work Done in Moving the Charge:
- The work done W in moving a charge q0 in an electric field is given by the change in electric potential energy:
W=q0(VB−VA)
- Since VA=VB, we have:
W=q0(kQr−kQr)=q0⋅0=0
5. Conclusion:
- The work done in moving the test charge q0 from point A to point B is zero.
Final Answer:
The work done in moving the test charge q0 from point A to point B is 0.
---
- We have a charge Q located at the center of a circle with radius r.
- Points A and B are located at opposite ends of the diameter of the circle.
- The electric potential V at any point in the electric field created by charge Q is given by the formula:
V=kQr
- Here, k=14πϵ0 is the Coulomb's constant.
- Since both points A and B are at the same distance r from the charge Q (as they are at the ends of the diameter), the electric potential at both points is the same:
VA=VB=kQr
- The work done W in moving a charge q0 in an electric field is given by the change in electric potential energy:
W=q0(VB−VA)
- Since VA=VB, we have:
W=q0(kQr−kQr)=q0⋅0=0
- The work done in moving the test charge q0 from point A to point B is zero.
The work done in moving the test charge q0 from point A to point B is 0.
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 2BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2EXERCISE - SECTION C
6 Videos
- QUESTION PAPER 2022 TERM 1 SET 2BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2EXERCISE - SECTION C
6 Videos
- QUESTION PAPER 2022 TERM 1 SET 1BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1EXERCISE - SECTION-C
6 Videos
- QUESTION PAPER 2023BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2023EXERCISE - Question
43 Videos
Similar Questions
Knowledge Check
In the firgure the charge Q is at the centre of the circle. Work done is maximum when another charge is taken from point P to
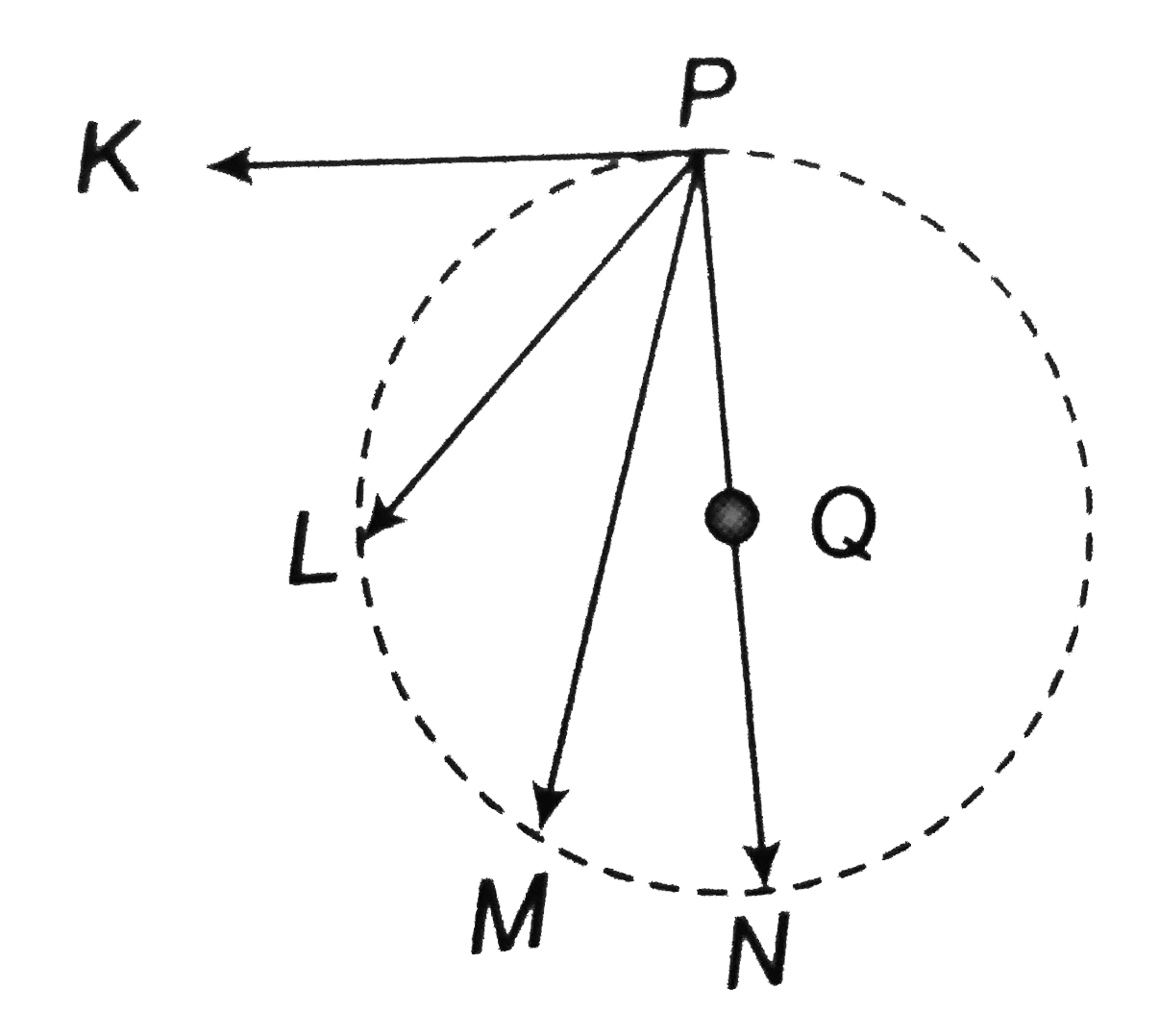 AKBLCMDN
AKBLCMDNCharge q2 is at the centre of a circular path with radius r. work done in carrying charge q1 once around this equipotential path , would be
A14πε0×q1q2r2B14πε0×q1q2rCzeroDInfinityThe work done in carrying a charge Q1 once round a circle of radius R with a charge Q2 at the centre is
A14πε0×q1q2r2B14πε0×q1q2rCzeroDInfinite
" A charge "q_(0)" is brought from infinity to the centre of a dipole.The work done is "
View SolutionA point charge Q is placed at the centre of a circular wire of radius R having charge q. Find the force of electrostatic interaction between point charge and the wire.
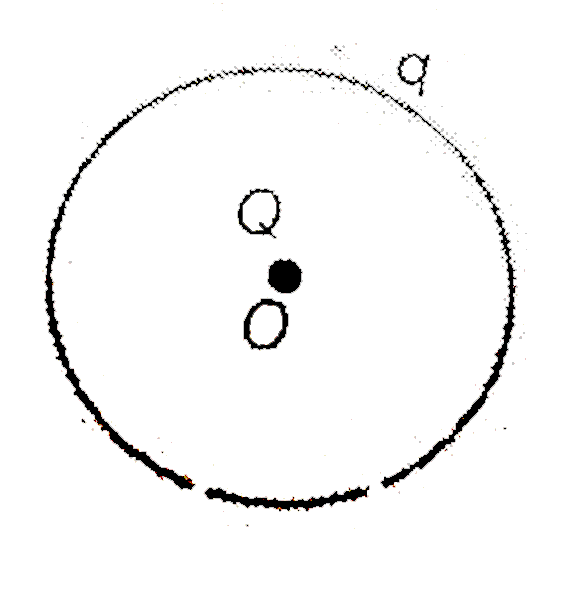
View SolutionOn rotating a point charge g around a charge Q in a circle of radius r, the work done is
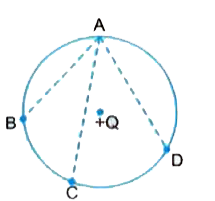
View SolutionIn the electric field of a point charge Q placed at the centre of a circle, as shown in fingure, a certain test charge q0 is carried from point A to B, C B and D. Then the work done
View SolutionA square of side a charge Q at its centre and charge q at one of the corners. The work required to be done in moving the charge q from the corner to the diagonally opposite corner is
View Solution