तीन प्रतिरोधकों R1,R2 एवं R3 को श्रेणीक्रम में जोड़ा गया है। समतुल्य प्रतिरोध R का व्यंजक होगा
(R1+R2)×R3
1R1+1R2+1R3
R1+R2+R3
इनमें से सभी। all ofthese
The correct Answer is:C
Step by step video, text & image solution for तीन प्रतिरोधकों R_(1), R_(2) एवं R_(3) को श्रेणीक्रम में जोड़ा गया है। समतुल्य प्रतिरोध R का व्यंजक होगा by Physics experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - JHARKHAND BOARD PREVIOUS YEAR PAPERSCHAPTER - ANNUAL EXAMINATION 2013EXERCISE - विज्ञान-प्रायोगिक खण्ड-अ7videos
ANNUAL EXAMINATION 2013
- BOOK - JHARKHAND BOARD PREVIOUS YEAR PAPERSCHAPTER - ANNUAL EXAMINATION - 2020EXERCISE - विज्ञानं GROUP - B2videos
ANNUAL EXAMINATION - 2020
- BOOK - JHARKHAND BOARD PREVIOUS YEAR PAPERSCHAPTER - ANNUAL EXAMINATION 2014EXERCISE - विज्ञान-प्रयोगिक खंड -B3videos
ANNUAL EXAMINATION 2014
Similar Questions
चित्र में परावर्तन कोण है
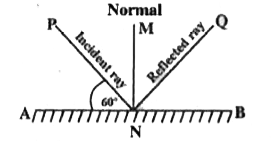 02:55View Solution
02:55View Solutionकौन से करक किसी समष्टि के आकर का निर्धारण करते हैं ? (उतर अधिकतम 40 शब्दो मे दीजिये )
03:29View Solutionजब 2Ω का प्रतिरोधक एक सेल के साथ जोड़ते है तो इसमें प्रवाहित होने वाली धारा का परिणाम 1A है। यदि 2Ω का एक अन्य प्रतिरोध का इस प्रतिरोधक के साथ श्रेणीक्रम में लगा दिया जाए तो धारा का परिणाम होगा
02:28View SolutionIf r_(1),r_(2),r_(3) are the radii of the escribed circlesof a Delta ABC and ifr is the radius of its incircle then r_(1)r_(2)r_(3)-r(r_(1)R_(2)+r_(2)r_(3)+r_(3)r_(1))=
10:10View Solutionr+r3+r1−r2=
02:29View Solutionshow that r2r3+r3r1+r1r2=s2
06:22View SolutionProve that r1(r2+r3)√r1r2+r2r3+r3r1=a
01:43View SolutionIf rr1=r2r3, then
08:11View SolutionStatement-1: ln !ABC,r1+r2+r3−r=4R
Statement-2: In !ABC,r1r2+r2r3+r3r1=!201:33View SolutionIf r,r1,r2,r3 have their usual meanings , the value of 1r1+1r2+1r3, is
03:37View SolutionProve the questions
a(rr1+r2r3)=b(rr2+r3r1)=c(rr3+r1r2)05:30View SolutionIf r1,r2,r3,r are in usual notation in ΔABC then r1r2r3−r(r1r2+r2r3+r3r1)=
03:37View Solutionतीन प्रतिरोधों 2Ω,4Ω,5Ω को श्रेणीक्रम में जोड़ा जाता है तथा इस संयोजन को 12 V वि.वा.बल एवं नगण्य आन्तरिक प्रतिरोध की एक बैटरी से जोड़ा गया है। इन प्रतिरोधों में विभव बिन्दु हैं
02:00View SolutionLet ABC be a triangle with incentre I and inradius r. Let D, E, F be the feet of the perpendiculars from I to the sides BC, CA and AB, respectively, If r2 and r3 are the radii of circles inscribed in the quadrilaterls AFIE, BDIF and CEID respectively, then prove that r1r−r1+r2r−r2+r3r−r3=r1r2r3(r−r1)(r−r2)(r−r3)
05:18View Solution(r2+r3)√rr1r2r3=
04:13View SolutionIf rr2=r1r3 then
02:07View Solution

