Doubtnut Promotions Sticky

Assertion (A) : If Assertion (A) : If 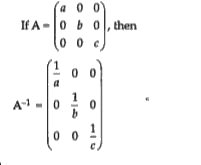Reason (R) : The inverse of a diagonal matrix is a diagonal matrix.
Reason (R) : The inverse of a diagonal matrix is a diagonal matrix.

A

Both (A) and (R) are true and R is the correct explanation A.

B

Both (A) and (R) are true but R is not correct explanation of A.

C

A is true but R is false.

D

A is false but R is true.

Text Solution
Verified by Experts

The correct Answer is:B

Doubtnut Promotions Banner
|
Updated on:21/07/2023
Class 12MATHSMATRICES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let A=[aij] be a square matrix of order n such that
    aij={0ifi≠jiifi=j
    Statement -2 : The inverse of A is the matrix B=[bij] such that
    bij={0ifi≠j1iifi=j
    Statement -2 : The inverse of a diagonal matrix is a scalar matrix.

    AStatement -1 is True, Statement -2 is true, Statement -2 is a correct explanation for Statement-1.
    BStatement-1 is True, Statement -2 is True, Statement -2 is not a correct explanation for Statement -1.
    CStatement -1 is True, Statement -2 is False.
    DStatement -1 is False, Statement -2 is True.
  • Question 2 - Select One

    Which of the following is a diagonal matrix ?

    A⎡⎢⎣234500067⎤⎥⎦
    B⎡⎢⎣023403670⎤⎥⎦
    C⎡⎢⎣200040008⎤⎥⎦
    DNone of these
  • Question 3 - Select One

    Which of the following is/are incorrect?
    (i) adjoint of a symmetric matrix is symmetric
    (ii) adjoint of a unit matrix is a unit matrix
    (iii) A(adjA)=(adjA)A=|A|I
    (iv) adjoint of a diagonal matrix is a diagonal matrix

    A(i)
    B(ii)
    C(iii) and (iv)
    Dnone of these