Assertion (A) : 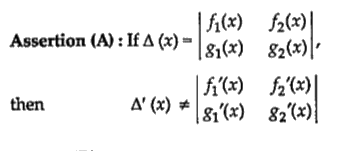
Reason (R) : ddx{f(x)g(x)}≠ddxf(x)ddxg(x).
Both (A) and (R) are true and R is the correct explanation A.
Both (A) and (R) are true but R is not correct explanation of A.
A is true but R is false.
A is false but R is true.
The correct Answer is:A
Similar Questions
If f(x)andg(x) are differentiate functions, then show that f(x)±g(x) are also differentiable such that ddx{f(x)±g(x)}=ddx{f(x)}±ddx{g(x)}
View SolutionIf f(x)andg(x) a re differentiate functions, then show that f(x)±g(x) are also differentiable such that ddx{f(x)±g(x)}=ddx{f(x)}±ddx{g(x)}
View Solution
Knowledge Check
∫[ddxf(x)]dx=
Af'(x)+cBf(x)+cC∫f(x)dxDef(x)+c
Using the first principle, prove that: ddx(f(x)g(x))=f(x)ddx(g(x))+g(x)ddx(f(x))
View SolutionIf f(x)andg(x) are two differentiable functions, show that f(x)g(x) is also differentiable such that ddx[f(x)g(x)]=f(x)ddx{g(x)}+g(x)ddx{f(x)}
View SolutionIf f(x)andg(f) are two differentiable functions and g(x)≠0 , then show that f(x)g(x) is also differentiable ddx{f(x)g(x)}=g(x)ddx{f(x)}−f(x)ddx{g(x)}[g(x)]2
View SolutionUsing the first principle, prove that: ddx(f(x)g(x))=f(x)ddx(g(x))+g(x)ddx(f(x))
View SolutionTheorem: ddx(∫f(x)dx)=f(x)
View SolutionIf f(x)=x2|x|, write ddx(f(x))
View SolutionIf f(x)andg(x) are two differentiable functions, show that f(x)g(x) is also differentiable such that ddx[f(x)g(x)]=f(x)ddx{g(x)}+g(x)ddx{f(x)}
View Solution
