An owner of an electric bike rental company have determined that if they charge customers < x per day to rent a bike, where 50≤x≤200, then number of bikes (n), they rent per day can be shown by linear function n(x) = 2000 - 10x. If they charge 50 per day or less, they will rent all their bikes. If they charge 200 or more per day, they will not rent any bike
Based on the above information, answer the following question.
At x = 260, then revenue collected by the company is:
10
500
0
1000
The correct Answer is:C
Topper's Solved these Questions
- APPLICATION OF CALCULUSBOOK - ICSECHAPTER - APPLICATION OF CALCULUSEXERCISE - Assertion and Reason based questions
5 Videos
- APPLICATION OF CALCULUS IN COMMERCE AND ECONOMICSBOOK - ICSECHAPTER - APPLICATION OF CALCULUS IN COMMERCE AND ECONOMICSEXERCISE - MULTIPLE CHOICE QUESTIONS (Choose the correct answer from the given four options in questions)
14 Videos
Similar Questions
Following frequency distribution gives the weights of 38 students of a class :
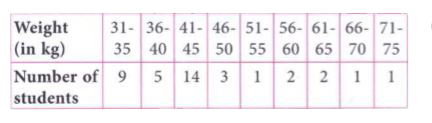
Based on the above information, answer the following questions.
Define an event whose probability is 1.
View SolutionAn architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200m as shown below:
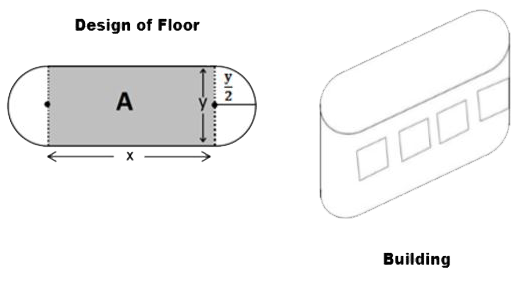
based on the above information answer the following
The CEO of the multi-national company is interested in maximizing the area of the whole floor including the semi-circular ends. For this to happen the valve of x should be
View Solution
Knowledge Check
A doctor is to visit a patient. From the past experience, it is known that the probabilities that the he will come by cab, metro, bike or by other means of transport are respectively 0.3, 0.2, 0.1 and 0.4. The probabilities that the he will be late are 0.25, 0.3, 0.35 and 0.1 if he vomes by cab, metro,bike and other means of transport respectively.

Based on the above information, answer the following questions.
When the doctor arrives late, what is the probability that he comes by bike ?A521B47C56D16Harsh made a piggy bank for himself using clay . If the shape of the bank is based on the function f (x)= | x - 4|+ | x - 5 | where f (x) represents the height of the bank
Based on the above information , answer the following questions :
For x>6 the value of the function f (x) isA1B−1C2x−9D2 x + 1A music concert is organised in a stadium that has a capacity of 36000 people . With ticket price of Rs. 10 the average attendance has been 24000 . Some financial expert estimated that price of a ticket should be determined by the function p(x)=15−x3000 , where x is the number of tickets sold
Based on the above information, answer the following questions
The value of x for which revenue is maximum , isA25000B22500C21000D20000
An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200m as shown below:

based on the above information answer the following
If x and y represents the length and breadth of the rectangular region, then the relation between the variables is
View SolutionAn architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200m as shown below:
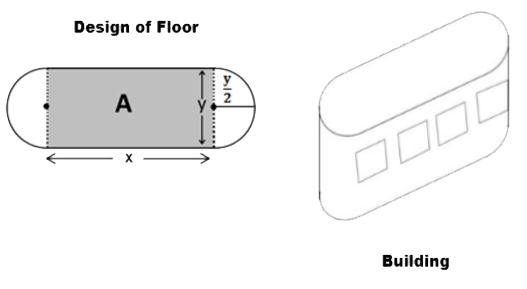
based on the above information answer the following
The extra area generated if the area of the whole floor is maximized is :
View SolutionHarsh made a piggy bank for himself using clay . If the shape of the bank is based on the function f (x)= | x - 4|+ | x - 5 | where f (x) represents the height of the bank
Based on the above information , answer the following questions :
The function | x| is
View SolutionSatellite TV manufacturing businesses tend to have what economists call "economies of scale." When economies of scale exist, bigness can be its own reward.
The more TV's you manufacture in a single run, lower the costs per unit, which in turn increases your bottom-line margins.
 Keeping that in mind, a T.V. manufacturing company increases its production uniformly by fixed number every year. The company produces 8000 sets in the 6th year and 11,300 sets in the 9th year.
Keeping that in mind, a T.V. manufacturing company increases its production uniformly by fixed number every year. The company produces 8000 sets in the 6th year and 11,300 sets in the 9th year.
On the basis of the above information, answer any four of the following questions:
The company's production of the first year is:
View SolutionAn architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200m as shown below:
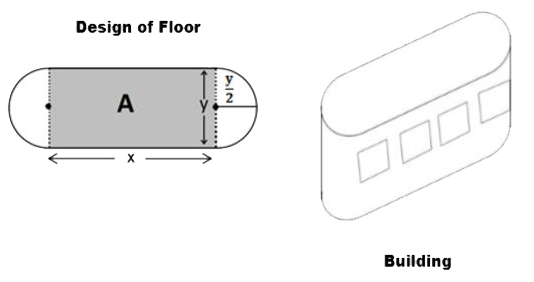
based on the above information answer the following
The maximum value of area A is
View Solution
