Define the collection {E1,E2,E3,.....} of ellipses and {R1,R2,R3,.....} of rectangles as follows:
E1=x29+y24=1 ,
R1 : rectangle of largest area, with sides parallel to the axes, inscribed in E1 ,
En : ellipse x2a2n+y2b2n=1 of largest are inscribed in Rn−1,n>1.
then which of the following options is/are corrct?
The eccentricities of E18andE19 are NOT equal
N∑n=1 (area of Rn ) < 24, for each positive integer N
The length of latus rectum of E9 is 16
The distance of a focus from the centre in E9 is √532
Step by step video & image solution for Define the collection {E_1,E_2,E_3,"....."} of ellipses and {R_1,R_2,R_3,"....."} of rectangles as follows: E_1= (x^2)/(9)+(y^2)/(4)=1 , R_1 : rectangle of largest area, with sides parallel to the axes, inscribed in E_1 , E_n : ellipse (x^2)/(a_(n)^(2))+(y^2)/(b_(n)^(2))=1 of largest are inscribed in R_(n-1), n gt 1. then which of the following options is/are corrct? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
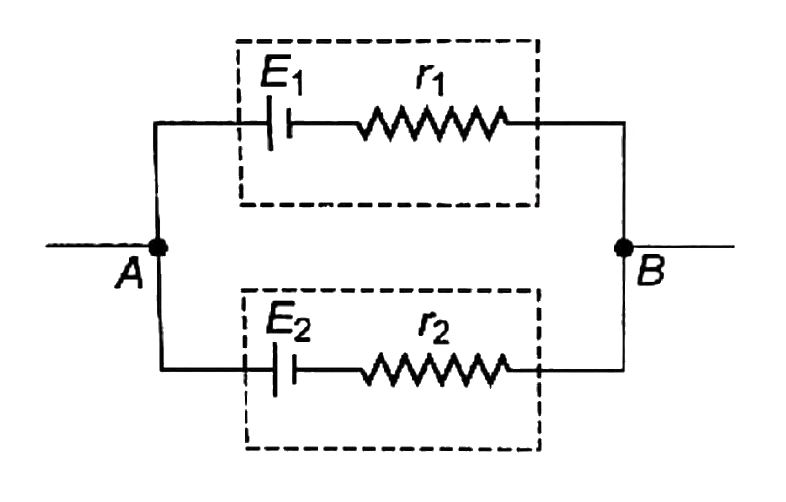
Two batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
View SolutionThe ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinates axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The length (in units) of the major axis of ellipse E2 is
View Solution
Knowledge Check
Define the collections {E1,E2,E3,...} of ellipses and {R1,R2,R3,...} of rectangles as follows :
E1:x29+y24=1
R1: rectangle of largest area, with sides parallel to the axes, inscribed in E1,
Rn−1,n>1,
Rn : rectangle of largest area, with sides parallel to the axes, inscribed in En>1.
Then which of the following options is /are correct ?Athe eccentricities of E18 and E19 are NOT equal.BThe distance of a locus from the centre in E9is√532.CN∑n=1(area of Rn)<24, for each positive integer N.DThe length of latusrectum of E9is16.For the batteries shown in fig. R1,R2andR3 are the internal resistance of E1,E2,andE3, respectively Then, which of the following is / are correct?
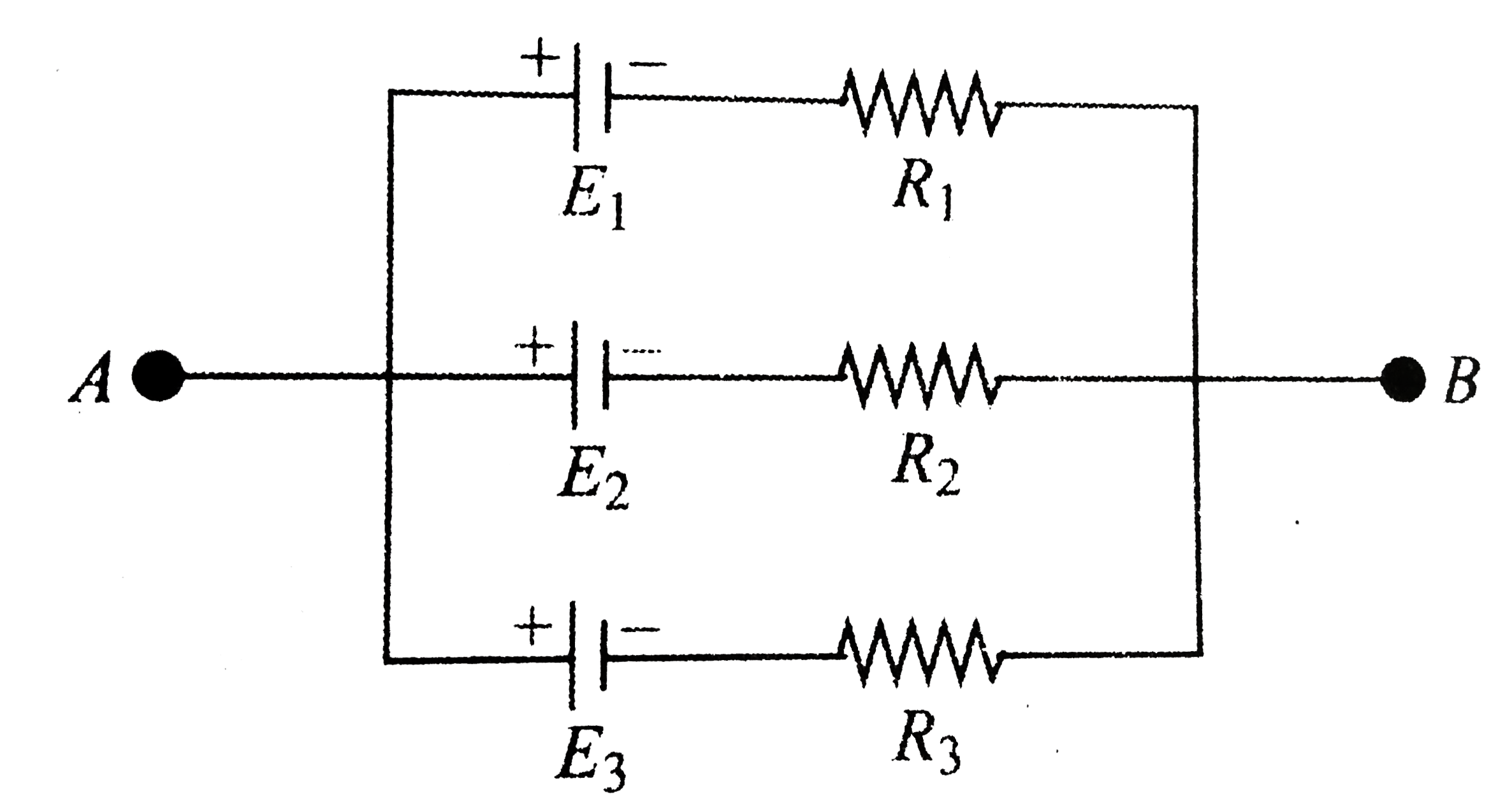 AThe equivalent internal resistance R of the system is given by (R1R2R3)/(R1R2+R2R3+R3R1).BIf E3=(E1R2+E2R1)/(R1+R2), the equivalent emf of the batteries will be equal to E3CThe equivalent emf to the battery is equal to E=(E1+E2+E3)/3DThe equivalent emf of the battery not only depends upon values of E1,E2,andE3 but also depends upon values of R1,R2andR3.
AThe equivalent internal resistance R of the system is given by (R1R2R3)/(R1R2+R2R3+R3R1).BIf E3=(E1R2+E2R1)/(R1+R2), the equivalent emf of the batteries will be equal to E3CThe equivalent emf to the battery is equal to E=(E1+E2+E3)/3DThe equivalent emf of the battery not only depends upon values of E1,E2,andE3 but also depends upon values of R1,R2andR3.Equation of ellipse E1 is x29+y24=1, A rectangle R1, whose sides are parallel to co-ordinate axes is inscribed in E1 such that its area is maximum now En is an ellipse inside Rn−1 such that its axes is along co-ordinate axes and has maxmim possible area ∀n≥2,n∈N, further Rn is a rectangle whose sides are parallel to co-ordinate axes and is inscribed in En−1. Having maximum area ∀n≥2,n∈N
Am∑n=1 area of rectangle (Rn)<24∀m∈NBLength of latus rectum of E9=16CDistance between focus and centre of E9=√532DThe eccentricities of E18 and E19 are not equal.
The ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
View SolutionIf e1 and e2 are respectively the eccentricities of the ellipse x218+y24=1 and the hyperbola x29−y24=1, then the relation between e1 and e2, is
View SolutionIf (1+px+x2)n=1+a1x+a2x2+…+a2nx2n.
Which of the following is true for 1<r<2n
View SolutionIf the length of latusrectum of ellipse E1:4(x+y+1)2+2(x−y+3)2=8 and E2=x2p+y2p2=1,(0<p<1) are equal , then area of ellipse E2, is
View SolutionA series of concentric ellipse E1,E2,E3,…,En is constructed as follows: Ellipse En touches the extremities of the major axis of En−1 and have its focii at the extremities of the minor axis of En−1. If eccentricity of ellipse En is en, then the locus of (e2n,e2n−1) is
View Solution
