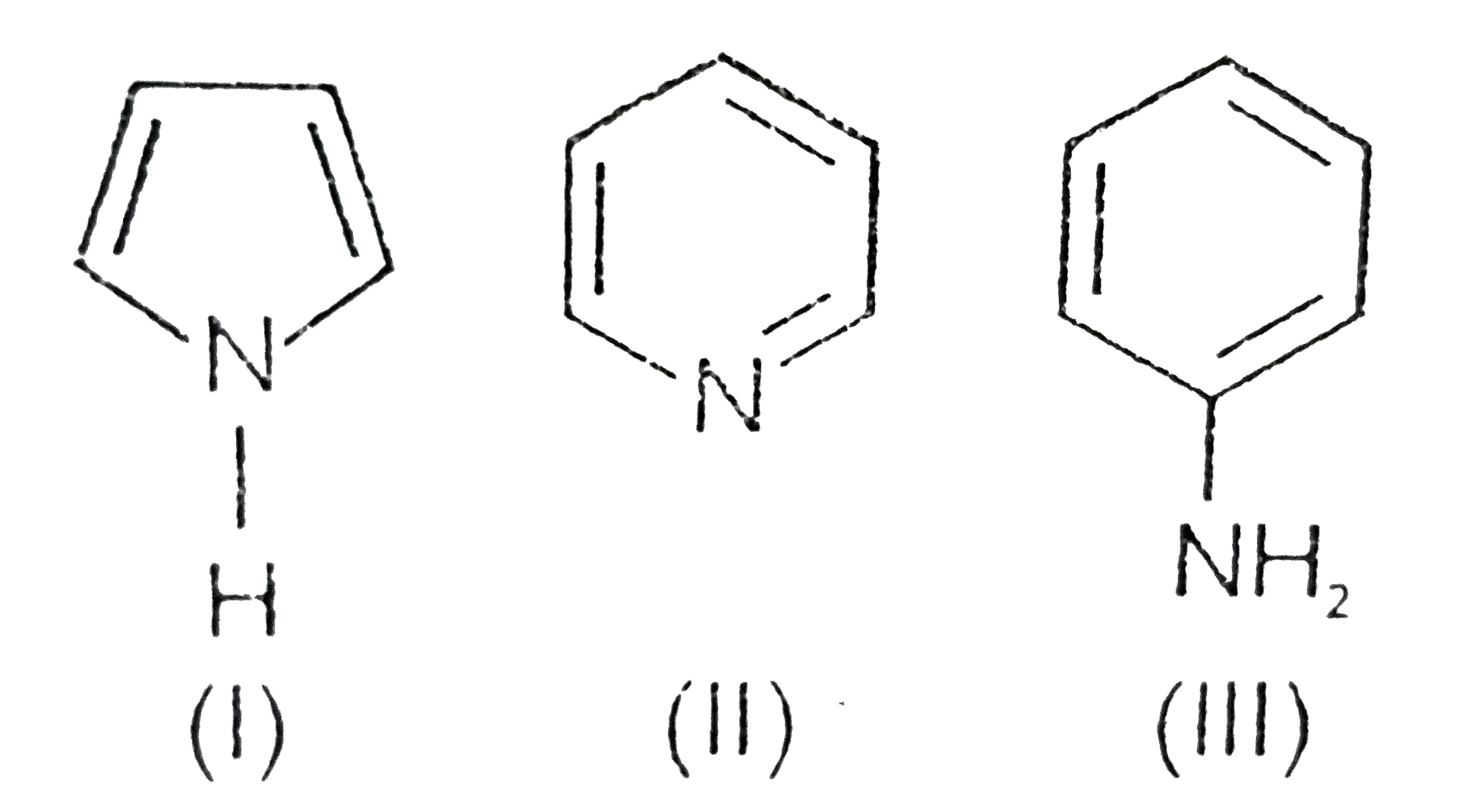
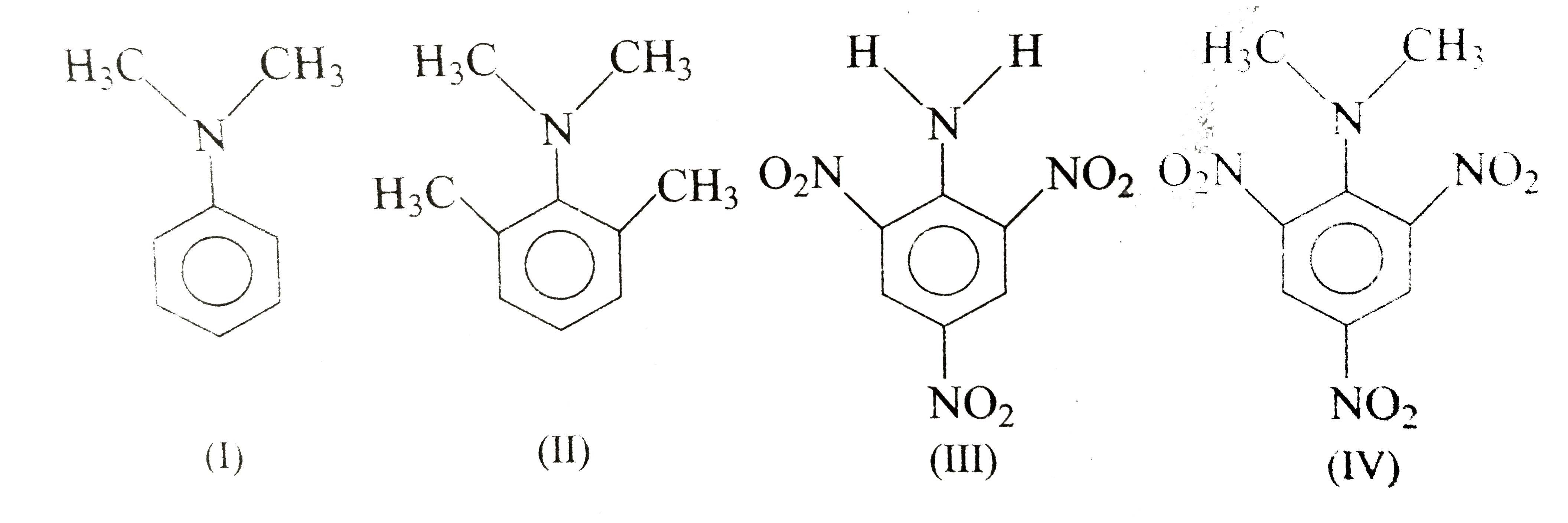
Let us consider a system of units in which mass and angular momentum are dimensionless. If length has dimension of L, which of the following statement(s) is/are correct?
The dimension of linear momentum is L−1
The dimension of energy is L−2
The dimension of force is L−3
The dimension of power is L−5
To solve the problem, we need to analyze the dimensions of various physical quantities under the assumption that mass and angular momentum are dimensionless, and length has a dimension of L.
1. Understanding the Given Information:
- Mass (M) and Angular Momentum (J) are dimensionless.
- Length (L) has a dimension of L.
2. Dimensional Formula of Mass:
- The dimensional formula of mass is represented as (M).
- Since mass is dimensionless in this system, we can write:
(M)=L0T0
3. Dimensional Formula of Angular Momentum:
- Angular momentum (J) is given by the formula J=M⋅V⋅R (where V is velocity and R is the distance).
- The dimensional formula for velocity (V) is LT−1 and for distance (R) is L.
- Thus, the dimensional formula for angular momentum is:
(J)=(M)⋅(V)⋅(R)=(M)⋅(LT−1)⋅L=(M)⋅L2T−1
- Since mass is dimensionless, we have:
(J)=L2T−1
4. Equating Dimensions:
- Since both mass and angular momentum are dimensionless, we can equate their dimensions:
L0T0=L2T−1
- This implies:
- L2=1 (which is not possible unless L is dimensionless)
- T−1=1 (which implies T is also dimensionless)
5. Analyzing Other Quantities:
- Linear Momentum (P):
- The formula for linear momentum is P=M⋅V.
- Thus, (P)=(M)⋅(V)=(M)⋅(LT−1).
- Since M is dimensionless, (P)=LT−1.
- In our dimensionless system, we can express this as (P)=L−1.
- Energy (E):
- Energy is defined as work done, which is force times distance.
- The formula for force is F=M⋅A where A=LT−2.
- Thus, (F)=(M)⋅(LT−2)=LT−2.
- Therefore, (E)=(F)⋅(D)=(LT−2)⋅L=L2T−2.
- In our dimensionless system, we can express this as (E)=L−2.
- Force (F):
- From the previous calculation, we have (F)=LT−2.
- In our dimensionless system, we can express this as (F)=L−3.
- Power (P):
- Power is defined as work done per unit time.
- Thus, (P)=(E)⋅(T−1)=(L2T−2)⋅T−1=L2T−3.
- In our dimensionless system, we can express this as (P)=L−4.
6. Conclusion:
- The dimensions of the quantities are:
- Linear Momentum: L−1
- Energy: L−2
- Force: L−3
- Power: L−4
Final Answer:
- The correct statements are:
- The dimension of linear momentum is L−1.
- The dimension of energy is L−2.
- The dimension of force is L−3.
- The dimension of power is incorrect as L−4.
- Mass (M) and Angular Momentum (J) are dimensionless.
- Length (L) has a dimension of L.
- The dimensional formula of mass is represented as (M).
- Since mass is dimensionless in this system, we can write:
(M)=L0T0
- Angular momentum (J) is given by the formula J=M⋅V⋅R (where V is velocity and R is the distance).
- The dimensional formula for velocity (V) is LT−1 and for distance (R) is L.
- Thus, the dimensional formula for angular momentum is:
(J)=(M)⋅(V)⋅(R)=(M)⋅(LT−1)⋅L=(M)⋅L2T−1
- Since mass is dimensionless, we have:
(J)=L2T−1
- Since both mass and angular momentum are dimensionless, we can equate their dimensions:
L0T0=L2T−1
- This implies:
- L2=1 (which is not possible unless L is dimensionless)
- T−1=1 (which implies T is also dimensionless)
- Linear Momentum (P):
- The formula for linear momentum is P=M⋅V.
- Thus, (P)=(M)⋅(V)=(M)⋅(LT−1).
- Since M is dimensionless, (P)=LT−1.
- In our dimensionless system, we can express this as (P)=L−1.
- Energy is defined as work done, which is force times distance.
- The formula for force is F=M⋅A where A=LT−2.
- Thus, (F)=(M)⋅(LT−2)=LT−2.
- Therefore, (E)=(F)⋅(D)=(LT−2)⋅L=L2T−2.
- In our dimensionless system, we can express this as (E)=L−2.
- From the previous calculation, we have (F)=LT−2.
- In our dimensionless system, we can express this as (F)=L−3.
- Power is defined as work done per unit time.
- Thus, (P)=(E)⋅(T−1)=(L2T−2)⋅T−1=L2T−3.
- In our dimensionless system, we can express this as (P)=L−4.
- The dimensions of the quantities are:
- Linear Momentum: L−1
- Energy: L−2
- Force: L−3
- Power: L−4
- The correct statements are:
- The dimension of linear momentum is L−1.
- The dimension of energy is L−2.
- The dimension of force is L−3.
- The dimension of power is incorrect as L−4.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Consider the reactions shown below:
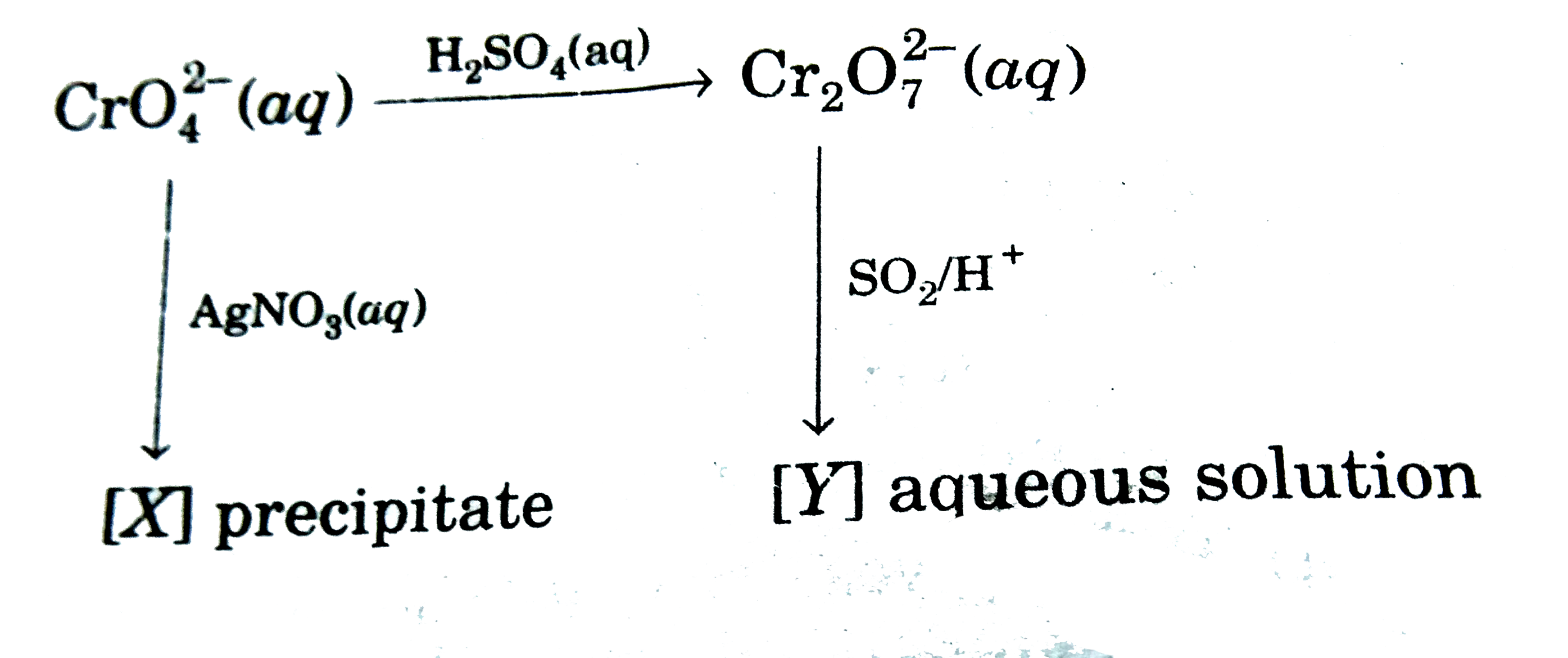
which of the following statement(s) is/are correct?A[X] is a yellow coloured precipitateB[X] is soluble in ammonia solutionC[Y] is given green coloured solution with excess of sodium hydroxide solutionDThe conversion of Cr2O2−7 to [Y] is a redox reactionConsider the reactions shown below:

Which of the following statement (s) is/are correct?A[X] is a yellow coloured precipitate.B[X] is soluble in ammonia solutionC[Y] gives green coloured solution with excess of sodium hydroxide solution.DThe conversion of Cr2O2−7 to [Y] is an redox reaction.Consider the following reaction,
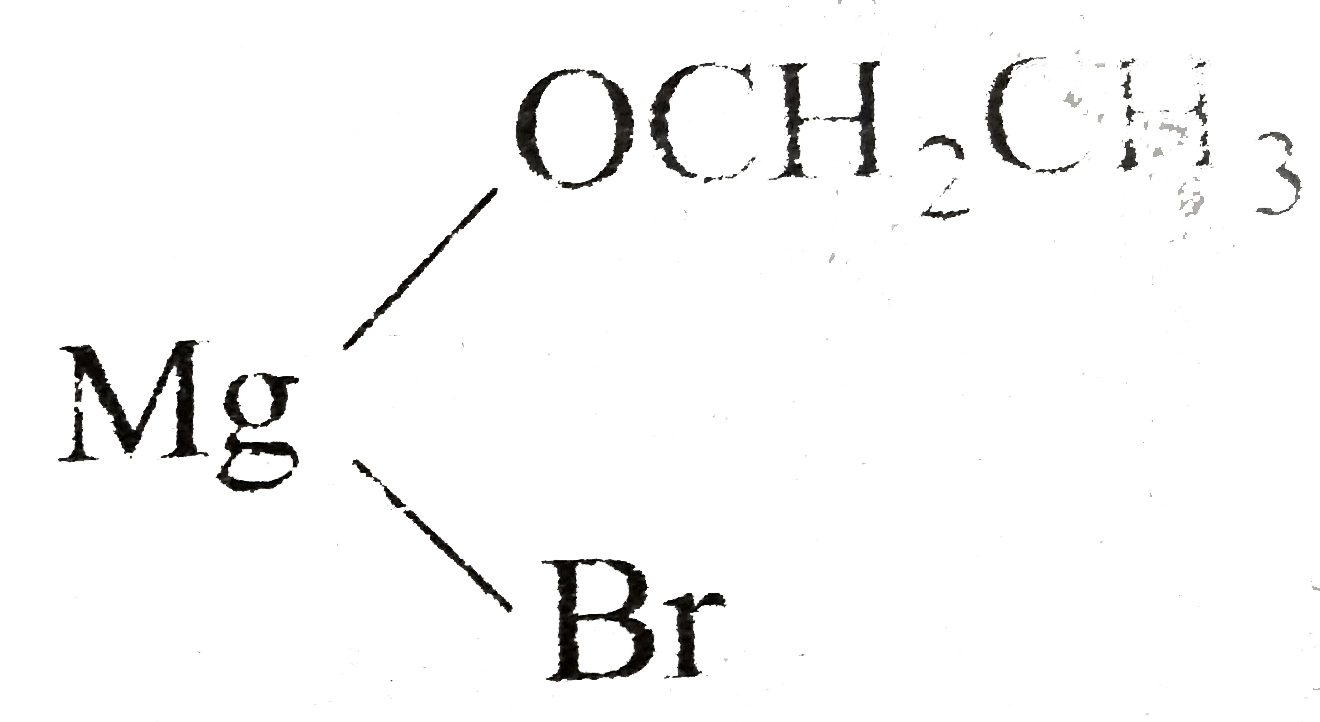 which of
which of
the following statements is (are) correct ?ACH3CH2OH+CH3CH2H∗ comes from the Grignard reagent.BH∗ in CH3CH2H∗ comes from the Grignard reagent .CH∗ in CH3CH2H∗ comes from ethanol.DH∗ in CH3CH2H∗ comes from the alkyl group of alcohol.
Which of the following statement(s) is/are correct about angular nodes
View SolutionConsider the following reactions :
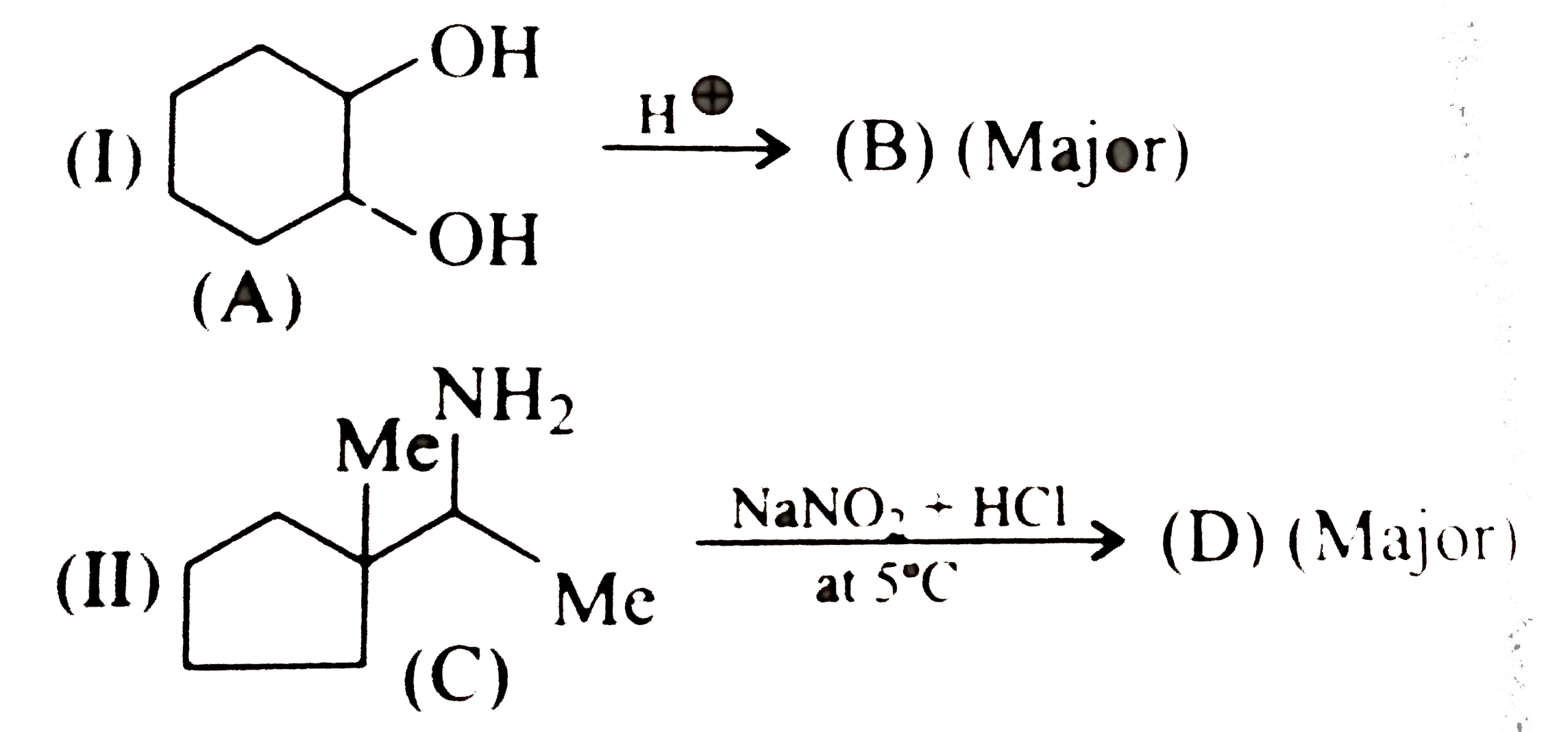
Which of the following statements are correct ?
View SolutionConsider the following reactions :
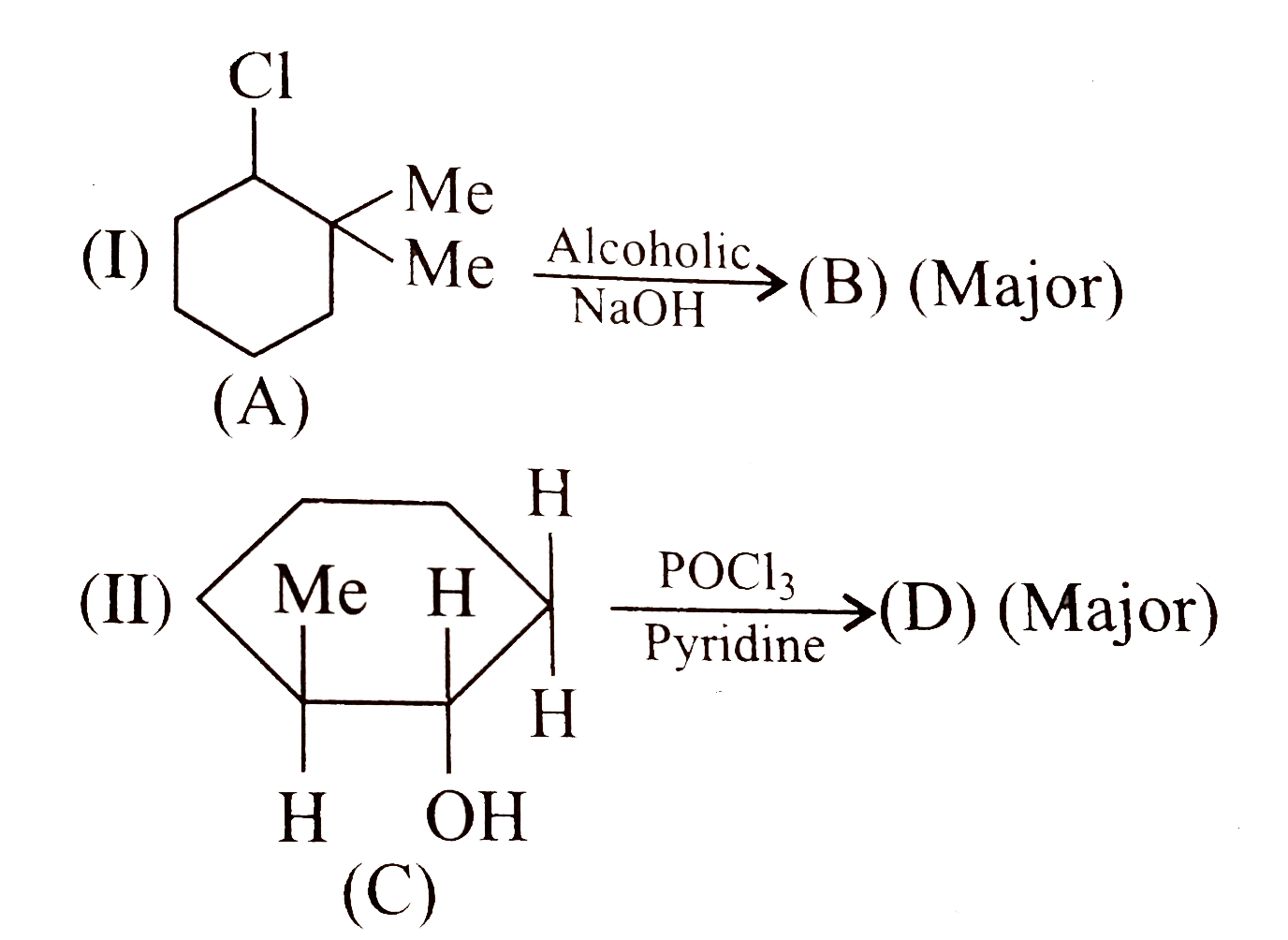
Which of the following statements are correct ?
View SolutionIf in a hypothetical system if the angular momentum and mass are dimensionless. Then which of the following is true.
View SolutionUsing the principle of homogeneity of dimensions, which of the following is correct?
View Solution