A solenoid of radius R and length L has a current I=I0 cosωt. The value of induced electric field at a distance of r outside the solenoid, is
μ0nI0ωR22rsinωt
μ0nI0ωR2rsinωt
μ0nI0R22rsinωt
Zero
The correct Answer is:A
According to question:
(πR2)dBdt=2πrE
where B=μ0nI
Therefore E=μ0nI0ωR22rsinωt
Topper's Solved these Questions
Similar Questions
A cylindrical conductor of radius 'R' carries a current 'i'. The value of magnetic field at a point which is R/4 distance inside from the surface is 10T. Find the value of magnetic field at point which is 4R distance outside from the surface
View SolutionA tightly- wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current I n dx. (a) Write the magnetic field at the centre of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the centre of the solenoid. (b) Verify that if l>>a, the field tends to (B=(μ0)ni) and if a>>1, the field tends toB=((μ0)nil2a) . Interpret these results.
View Solution
Knowledge Check
- Question 1 - Select One
A solenoid of radius R number of turn per unit length n and length L has a current I=I0cosωt. The value of induced electric field at a distance of r outside the solenoid, is :
Aμ0nI0ωR22rsinωtBμ0nI0ωR2rsinωtCμ0nI0R22rsinωtDzero - Question 2 - Select One
A long solenoid of radous R has n turns of wire per unit length and carries a time-varying current that varies sinusiodally as I=Imaxcosωt, where Imax is the maximum current and ω I the angular frequancy of the alternating current source (shows in Fig.)

The magnitude of the induced electric field inside tha solenoid, a distance r<R from its long central axis isA3μ0nImaxω2rsinωtBμ0nImaxω2rcosωtCμ0nImaxωrsinωtDμ0nImaxω2rsinωt - Question 3 - Select One
A solenoid of length 0.5 m has a radius of 1 cm and is made up of 500 turns. It carries a current of 5 A. The magnetic field inside the solenoid is
A3.14×10−3TB6.28×10−3TC9.14×10−3TD1.68×10−3T
A tightly wound solenoid of radius 'a' and length 'l' has n turns per unit length. It carries an electric current i. Magnetic field at a distance l4 from one of the end (inside the solenoid on its axis) is B=μ0ni(√5+3)√K for l=4a. Then find the value of K.
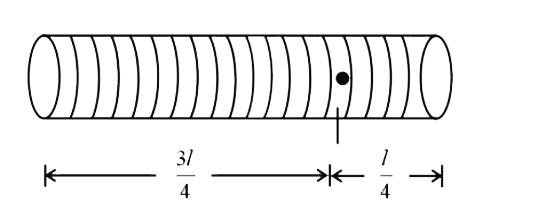 View Solution
View SolutionA long thin solenoid has 900tuns/metre and radius 2.50cm,. The current in the solenoid is increasing at a uniform rate of 60A/s. What is the magnitude of the induced electric field at a point?
a. 0.5cm from the axis of the solenoid.
b. 1.0cm from the axis of the solenoid.View SolutionThe cruuent in an ideal, long solenoid is varied at a uniform rate of 0.02A/s. The solenoid has 1000 turns/s and its radius is 8 cm.
(i) Consider a circle of radius 2 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 4 s.
(ii) Find the electric field induced at a point on the circumference of the circle.
(iii) Find the electric field induced at a point outside the solenoid at a distance 9 cm from its axis.View SolutionThe current in an ideal, long solenoid is varied at a uniform rate of 0.01As−1. The solenoid has 2000 turns/m and its radius 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. write the change in the magnetic flux through this circle in 2.0 seconds. (b) find the electric field induced at a point on the circumference of the circle. (c) find the electric field induced at a point outside the solenoid at a distance 8.0cm from its axis.
View SolutionA long solenoid of radius 4 cm, length 400 cmcarries a current of 3 A. The total number of turns is 100. Assuming ideal solenoid, find the flux passing through a circular surface having centre on axis of solenoid of radius 3 cm and is perpendicular to the axis of solenoid (i) inside and (ii) at the end of solenoid.
View Solution

