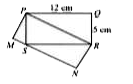
PQRS is are rectangle of dimensions 12 cm and 5 cm. PMNR is a rectangle drawn is such a way that the diagonal PR of the first rectangle is one of its sides and side opposie to it is touching the first rectangle at S as shown in figure. What is the ratio of the area of rectangle PQRS to that of PMNR?
The correct Answer is:C
Draw a line ST perpendicular to PR.
Since PQRS is a rectangle in , we have

(By Pythagoras theorem)
Now area of base height
Also
Area of rectangle
Area of rectangle PMNR=MN
Required ratio i.e. 1:1
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017-18 SET AEXERCISE - EVERYDAY MATHEMATICS10videos
IMO QUESTION PAPER 2017-18 SET A
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO MODEL TEST PAPER 2EXERCISE - ACHIEVERS SECTION5videos
IMO MODEL TEST PAPER 2
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017-18 SET-BEXERCISE - ACHIEVERS SECTION5videos
IMO QUESTION PAPER 2017-18 SET-B
Similar Questions
ABCD is a rectangle of dimensions 6 cm x 8 cm. DE and BF are the perpendiculars drawn on the diagonal of the rectangle. What is the ratio of the area of shaded to that of unshaded region?
View SolutionABCD is a rectangle of dimensions 6cm×8cm. DE and BF are the perpendiculars drawn on the diagonal of the rectangle what is the ratio of the shaded to that of unshaded region?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
ABCD is a rectangle of dimensions 8 units and 6 units AEFC is a rectangle drawn in such a way that diagonal AC of the first rectangle is one side and side opposite to it is touching the first rectangle at D as shown in the figure. What is the ratio of the area of rectangle ABCD to that of AEFC ?
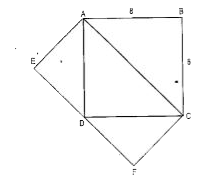 A2B3/2C1D8/9
A2B3/2C1D8/9 - Question 2 - Select One
If a diagonal of a rectangle is thrice its smaller side, then its length and breadth are in the ratio 3:1 (b) √3 :1 (c) √2 :1 (d) 2√2 :1
A√3:1B3:2C2√2:1D√2:1 - Question 3 - Select One
The perimeter of a rectangle is 60 cm and its breadth is 12 cm. What is the area of the rectangle?
A261cms2B263cms2C213cms2D216cms2
What is the length of a diagonal of a rectangle whose sides are 5 cm and 12 cm long?
View SolutionA circular wire of diameter 42 cm is bent in the form of a rectangle whose sides are in the ratio 6 : 5. Find the area of the rectangle.
View SolutionThe figure shows rectangle PQRS of 10 cm length and 8 cm width.
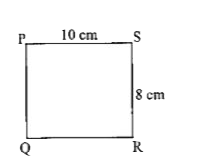
What is the perimeter of the given rectangle?View SolutionThe length and breadth of a rectangle is 16 cm and 12 cm. What will be the area of the rectangle?
View SolutionWhat is the area of a rectangle if its diagonal is 51 cm and one of its sides is 24 cm
View Solution

