It is known that if a+b=10, then a+b−c=10−c. State the Euclid's axiom that best illustrates this statement.
If equals be subtracted from equals, the remainders are equal.
Things which are halves of the same thing are equal to one other.
The whole is greater than the part.
None of these
The correct Answer is:A
To solve the question, we need to identify the Euclid's axiom that best illustrates the statement given: "If a+b=10, then a+b−c=10−c."
1. Understanding the Given Statement:
We have the equation a+b=10. This means that the sum of a and b is equal to 10.
2. Manipulating the Equation:
From the equation a+b=10, we can subtract c from both sides of the equation. This gives us:
a+b−c=10−c
This shows that if we take away c from both sides, the equality still holds.
3. Identifying the Axiom:
The axiom that best illustrates this property is known as the "Axiom of Equality." This axiom states that if two quantities are equal, then subtracting the same quantity from both sides will yield equal results.
In Euclid's terms, this can be summarized as:
- "Things which are equal to the same thing are equal to one another."
4. Conclusion:
Therefore, the Euclid's axiom that best illustrates the statement is that if a+b=10, then subtracting c from both sides maintains the equality, which can be expressed as:
- "If a=b and b=c, then a=c."
We have the equation a+b=10. This means that the sum of a and b is equal to 10.
From the equation a+b=10, we can subtract c from both sides of the equation. This gives us:
a+b−c=10−c
This shows that if we take away c from both sides, the equality still holds.
The axiom that best illustrates this property is known as the "Axiom of Equality." This axiom states that if two quantities are equal, then subtracting the same quantity from both sides will yield equal results.
- "Things which are equal to the same thing are equal to one another."
Therefore, the Euclid's axiom that best illustrates the statement is that if a+b=10, then subtracting c from both sides maintains the equality, which can be expressed as:
- "If a=b and b=c, then a=c."
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017 SET BEXERCISE - EVERYDAY MATHEMATICS10videos
IMO QUESTION PAPER 2017 SET B
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017 SET BEXERCISE - ACHIEVERS SECTION5videos
IMO QUESTION PAPER 2017 SET B
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET BEXERCISE - Achievers section5videos
IMO QUESTION PAPER 2016 SET B
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET AEXERCISE - ACHIEVERS SECTION5videos
IMO QUESTION PAPER 2018 SET A
Similar Questions
Knowledge Check
- Question 1 - Select One
It is known that if x+y=10, then x+y+z=10+z. The Euclid's axiom that illustrates this statement is
Afirst axiomBsecond axiomCthird axiomDfourth axiom - Question 2 - Select One
Euclid s which axiom illustrates the statement that when x+y =15
AfirstBsecondCthirdDfourth - Question 3 - Select One
Find a : b : c, if 6a = 9b = 10c.
A12:10:8B15:4:3C15:18:9D15:10:9
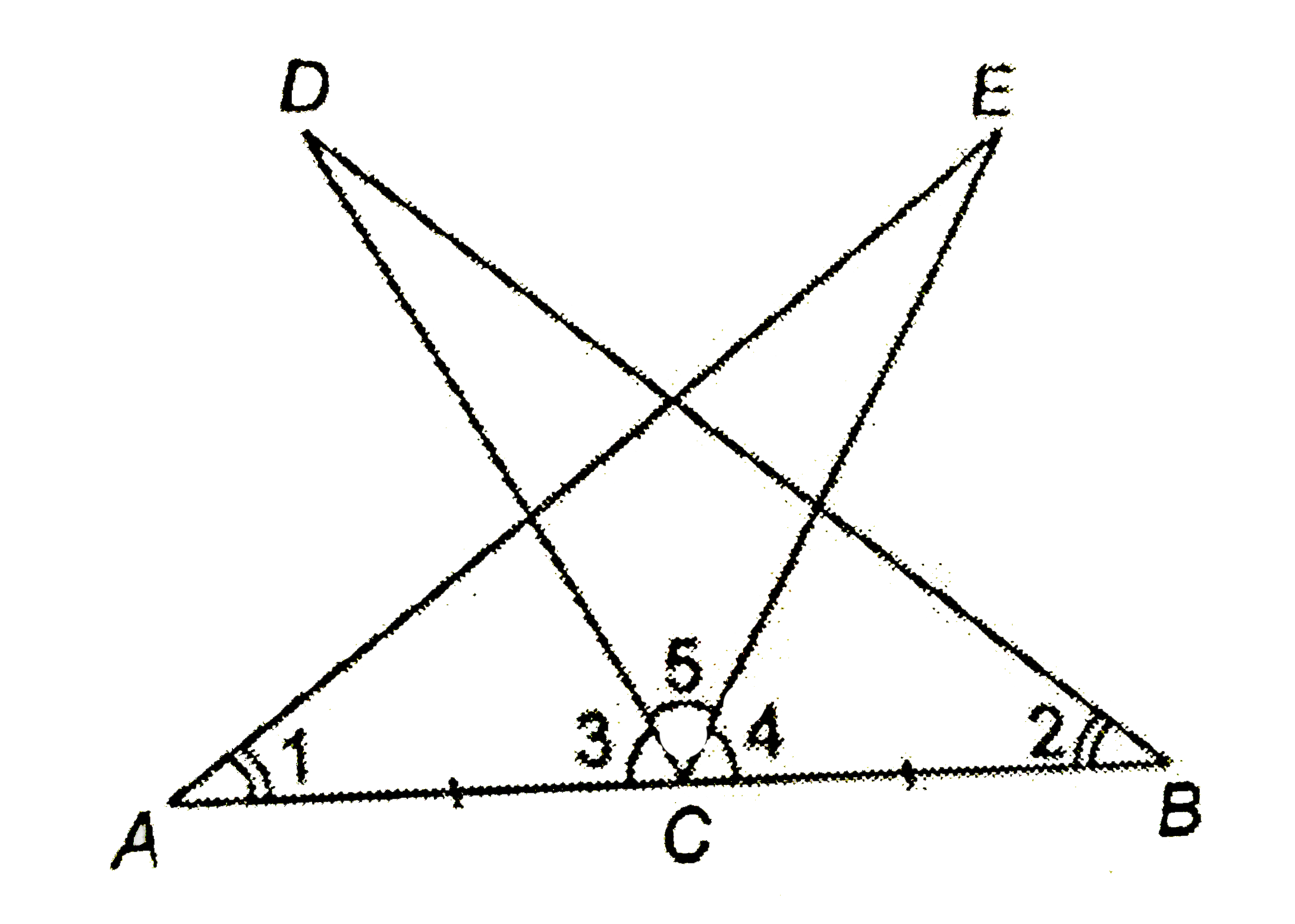
Use the information marked to prove :
(i) ΔEAC≅ΔDBC (ii) EC=DC
Also state the Euclid's axiom used in proving the congruency of two triangles.
 View Solution
View Solutiona(bc)=(ab)c. If N ordered triplets of integral Is (a,b,c) with −10≤a,b,c≤10 are there, Such that the given equation is a true statement, then find N120?
View SolutionInΔABC, it is known that∠B=∠C. Imagine you have another copy ofΔABC IsΔABC≅ΔACB State the three pairs of matching parts you have used to answer (i). Is it true to say that AB=AC?
View SolutionA is of the same age as B and C is of the same age as B Euclid 's which axiom illustrates the relative ages of A and C?
View SolutionThe usual form of 100a + b + 10c is
View Solution

