Find the value of m and n respectively
51m×n34=20
3,1
3,3
4,1
5,3
The correct Answer is:B
To solve the equation 51m×n34=20, we will follow these steps:
Step 1: Convert Mixed Numbers to Improper Fractions
The mixed number 51m can be converted to an improper fraction:
51m=5m+1m
Similarly, n34 can be expressed as:
n34=4n+34
Step 2: Rewrite the Equation
Now, we can rewrite the equation using the improper fractions:
5m+1m×4n+34=20
Step 3: Simplify the Equation
To eliminate the fraction, we can multiply both sides by 4m:
(5m+1)(4n+3)=80m
Step 4: Expand the Left Side
Expanding the left side gives:
20mn+15m+4n+3=80m
Step 5: Rearrange the Equation
Rearranging the equation to bring all terms to one side results in:
20mn+4n+15m+3−80m=0
which simplifies to:
20mn+4n−65m+3=0
Step 6: Solve for Values of m and n
At this point, we can try different integer values for m and n to find a solution.
Let's try m=3 and n=1:
20(3)(1)+4(1)−65(3)+3=60+4−195+3=−128(not a solution)
Next, let's try m=3 and n=3:
20(3)(3)+4(3)−65(3)+3=180+12−195+3=0(this works!)
Thus, the values of m and n are:
m=3,n=3
Final Answer
The values of m and n are 3 and 3 respectively.
---
The mixed number 51m can be converted to an improper fraction:
51m=5m+1m
Similarly, n34 can be expressed as:
n34=4n+34
Now, we can rewrite the equation using the improper fractions:
5m+1m×4n+34=20
To eliminate the fraction, we can multiply both sides by 4m:
(5m+1)(4n+3)=80m
Expanding the left side gives:
20mn+15m+4n+3=80m
Rearranging the equation to bring all terms to one side results in:
20mn+4n+15m+3−80m=0
which simplifies to:
20mn+4n−65m+3=0
At this point, we can try different integer values for m and n to find a solution.
20(3)(1)+4(1)−65(3)+3=60+4−195+3=−128(not a solution)
20(3)(3)+4(3)−65(3)+3=180+12−195+3=0(this works!)
m=3,n=3
The values of m and n are 3 and 3 respectively.
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - FRACTIONS EXERCISE - Everyday Mathematics5videos
FRACTIONS
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - FRACTIONS EXERCISE - Achievers Section (Hots)5videos
FRACTIONS
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - DECIMALS EXERCISE - Achievers Section (Hots)5videos
DECIMALS
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO MODEL TEST PAPER 1 EXERCISE - ACHIEVERS SECTION5videos
IMO MODEL TEST PAPER 1
Similar Questions
Knowledge Check
- Question 1 - Select One
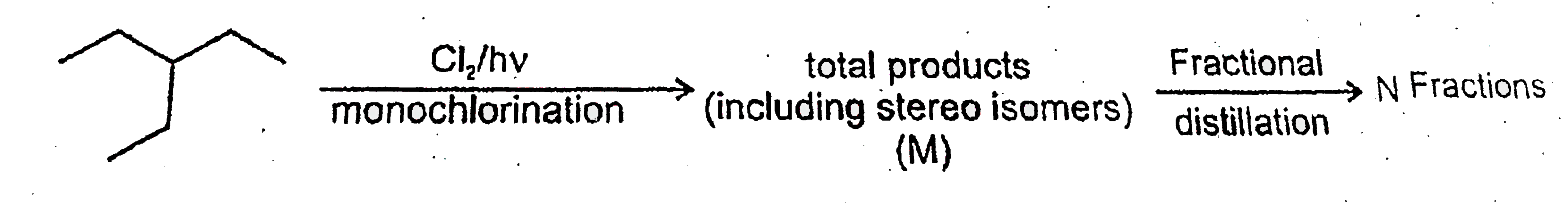
The value of M and N are respectively.A3.2B3,3C4,3D3,4 - Question 2 - Select One
Find the value of (−4m)3÷1(2m)2
A−16mB−256m5C−125m6D125m6 - Question 3 - Select One
Find the value of m so that (−3)m^(+1)×(−3)5=(−3)7
A1B−1C0D4
Find the value of m :
6m−4=1View SolutionFind the value of m
m−13−m−24=1View SolutionFind the value of m for which 5m÷5−3=55.
View SolutionIf A(2,3,−4),B(m,1,−1),C(3,2,2)andG(3,2,n) is the centroid of ΔABC, then the values of m and n respectively are
View SolutionThe values of m, n respectively, if 108=2m×33×5n, are:
View Solution

