A group consists of 15 males and 12 females. Write a quadratic polynomial whose roots are equal to the number of males and females .
x2−27x+180
x2+27x−180
x2+3x−27
None of these
The correct Answer is:A
To find a quadratic polynomial whose roots are equal to the number of males (15) and females (12), we can follow these steps:
Step 1: Identify the roots
The roots of the polynomial are given as:
- α=15 (number of males)
- β=12 (number of females)
Step 2: Use the standard form of a quadratic polynomial
The standard form of a quadratic polynomial with roots α and β is given by:
P(x)=(x−α)(x−β)
Step 3: Substitute the roots into the polynomial
Substituting α and β into the polynomial gives:
P(x)=(x−15)(x−12)
Step 4: Expand the polynomial
Now, we will expand the expression:
P(x)=x2−12x−15x+180
P(x)=x2−27x+180
Final Polynomial
Thus, the quadratic polynomial whose roots are 15 and 12 is:
P(x)=x2−27x+180
The roots of the polynomial are given as:
- α=15 (number of males)
- β=12 (number of females)
The standard form of a quadratic polynomial with roots α and β is given by:
P(x)=(x−α)(x−β)
Substituting α and β into the polynomial gives:
P(x)=(x−15)(x−12)
Now, we will expand the expression:
P(x)=x2−12x−15x+180
P(x)=x2−27x+180
Thus, the quadratic polynomial whose roots are 15 and 12 is:
P(x)=x2−27x+180
Topper's Solved these Questions
- IMO QUESTION PAPER 2018 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET BEXERCISE - ACHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER 2018 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET BEXERCISE - ACHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER 2018 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET AEXERCISE - Achievers section
5 Videos
- IMO QUESTION PAPER 2019 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019 SET AEXERCISE - Achievers section
5 Videos
Similar Questions
Knowledge Check
Number of females/ males in India
A933B930C927D940Both male and female frogs have
ALong hindlimbs with five webbed fingersBShort forelimbs with four unwebbed fingersCBoth a and bDExternal earsMouth in male and female Ascaris is
ATerminalBVentralCTriradiateDBoth (1) & (3)
Rs. 180 are divided into 66 male and female. The ratio of total amount given to male and female is 5 : 4. The ratio of amount given to one male and female is 3 : 2.Find the number of males and females.
View SolutionThe bar graph shows the total number of male and female lives in four different towns and table shows the number of males and females whose ages are above 40 years. Read the data carefully and answer the questions below:
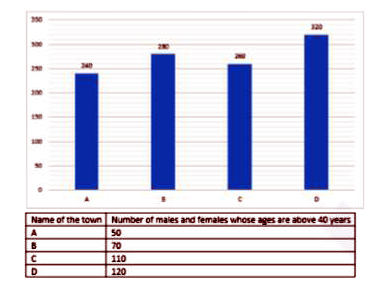
Find the ratio of the those number of males and females whose ages are above 40 years in town A and B to those males and females whose ages are below and equals to 40 years in town D.
View SolutionThe total numbers of males and females in a town is 70,000. If the number of males is increased by 6% and that of the females is increased by 4% , then the total numbers of males and females in the town would become 73520. Whatis the difference between the numberof males and females in the town, in the beginning?
View SolutionThe bar graph shows the total number of male and female lives in four different towns and table shows the number of males and females whose ages are above 40 years. Read the data carefully and answer the questions below:
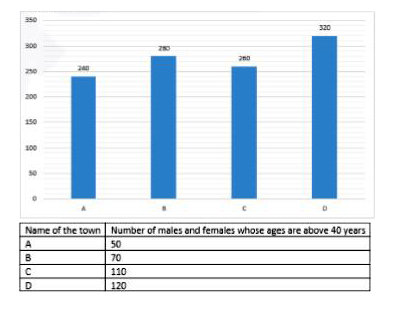
If in another town E, total males and females are 10% more than the total males and females in town A and those males and females whose ages are above 40 years is 20% more than those males and females whose ages are above 40 years in town C. find the number of those males and females in town E whose ages are below and equals to 40 years.
View SolutionThe bar graph shows the total number of male and female lives in four different towns and table shows the number of males and females whose ages are above 40 years. Read the data carefully and answer the questions below:
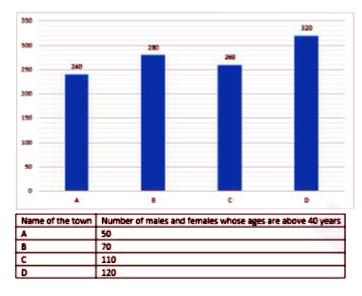
Number of males and females in town A whose ages are below and equals to 40 years is what percent less than those number of males and females in town D whose ages are below and equals to 40 years.
View Solution
