Ram, Raghav, Tarun and Varun together had a total amount of Rs 240 with them. Ram had half of the total amount that others had. Raghav had one-third of the total amount that others had. Tarun had one-fourth of the total amount that others had. Find the amount that Varun had.
Rs 64
Rs 70
Rs 52
Rs 58
The correct Answer is:C
To solve the problem step by step, let's denote the amounts that Ram, Raghav, Tarun, and Varun have as follows:
- Let Ram's amount be R
- Let Raghav's amount be G
- Let Tarun's amount be T
- Let Varun's amount be V
According to the problem, we have the following information:
1. The total amount they have together is R+G+T+V=240 (Equation 1).
2. Ram had half of the total amount that the others had:
R=12(G+T+V)(Equation 2)
3. Raghav had one-third of the total amount that the others had:
G=13(R+T+V)(Equation 3)
4. Tarun had one-fourth of the total amount that the others had:
T=14(R+G+V)(Equation 4)
Step 1: Solve for Ram's Amount
From Equation 1, we can express G+T+V in terms of R:
G+T+V=240−R
Substituting this into Equation 2:
R=12(240−R)
Multiplying both sides by 2 to eliminate the fraction:
2R=240−R
Adding R to both sides:
3R=240
Dividing by 3:
R=80
Step 2: Substitute Ram's Amount Back
Now that we have R=80, we can substitute this back into Equation 1 to find G+T+V:
G+T+V=240−80=160(Equation 5)
Step 3: Solve for Raghav's Amount
Using Equation 3:
G=13(R+T+V)=13(80+T+V)
Substituting T+V=160−G (from Equation 5):
G=13(80+160−G)
Multiplying by 3:
3G=80+160−G
Adding G to both sides:
4G=240
Dividing by 4:
G=60
Step 4: Substitute Raghav's Amount Back
Now substitute G=60 back into Equation 5 to find T+V:
T+V=160−60=100(Equation 6)
Step 5: Solve for Tarun's Amount
Using Equation 4:
T=14(R+G+V)=14(80+60+V)=140+V4
Substituting V=100−T (from Equation 6):
T=14(140+(100−T))
Multiplying by 4:
4T=140+100−T
Adding T to both sides:
5T=240
Dividing by 5:
T=48
Step 6: Find Varun's Amount
Now substitute T=48 back into Equation 6 to find V:
V=100−T=100−48=52
Final Answer
Thus, the amount that Varun had is 52.
- Let Raghav's amount be G
- Let Tarun's amount be T
- Let Varun's amount be V
2. Ram had half of the total amount that the others had:
R=12(G+T+V)(Equation 2)
3. Raghav had one-third of the total amount that the others had:
G=13(R+T+V)(Equation 3)
4. Tarun had one-fourth of the total amount that the others had:
T=14(R+G+V)(Equation 4)
G+T+V=240−R
R=12(240−R)
Multiplying both sides by 2 to eliminate the fraction:
2R=240−R
Adding R to both sides:
3R=240
Dividing by 3:
R=80
G+T+V=240−80=160(Equation 5)
G=13(R+T+V)=13(80+T+V)
Substituting T+V=160−G (from Equation 5):
G=13(80+160−G)
Multiplying by 3:
3G=80+160−G
Adding G to both sides:
4G=240
Dividing by 4:
G=60
T+V=160−60=100(Equation 6)
T=14(R+G+V)=14(80+60+V)=140+V4
Substituting V=100−T (from Equation 6):
T=14(140+(100−T))
Multiplying by 4:
4T=140+100−T
Adding T to both sides:
5T=240
Dividing by 5:
T=48
V=100−T=100−48=52
Topper's Solved these Questions
- IMO QUESTION PAPER 2019 SET BBook:SCIENCE OLYMPIAD FOUNDATION Chapter:IMO QUESTION PAPER 2019 SET BExercise:ACHIEVERS SECTION
Explore 5 Videos
- IMO QUESTION PAPER 2019 SET BBook:SCIENCE OLYMPIAD FOUNDATION Chapter:IMO QUESTION PAPER 2019 SET BExercise:ACHIEVERS SECTION
Explore 5 Videos
- IMO QUESTION PAPER 2019 SET ABook:SCIENCE OLYMPIAD FOUNDATION Chapter:IMO QUESTION PAPER 2019 SET AExercise:Achievers section
Explore 5 Videos
- IMO QUESTION PAPER 2020 SET 1Book:SCIENCE OLYMPIAD FOUNDATION Chapter:IMO QUESTION PAPER 2020 SET 1Exercise:Achievers Section
Explore 5 Videos
Similar Questions
Ram, Shyam, and Tarun have a total of Rs 600 with them. The amount with Ram is equal to half of the total amount with the others. Find the amount with Ram (in Rs)
View SolutionSonika spent 45760 on the interior decoration for her home, 27896 on buying air conditioner and the remaining 28% of the total amount she had as cash with her. What was the total amount?
View Solution
Knowledge Check
Amar. Bhavan. Chetan and Dinest have a total of Rs. 150 with them. Amar has one-fourth of the total amount with the others. The amount with Amar (in Rs) is:
A25B20C37.5D30Ram, Shyam, and Tarun have a total of Rs 600 with them. The amount with Ram is equal to half of the total amount with the others. Find the amount with Ram (in Rs)
A150B300C120D200Three persons A, B and C had Rs360 altogether. A transferred half of the amount he had to B, and C transferred half of the amount he had to A. After the transfer, all of them have equal amounts. What is the total amount B had before the transfer?
तीन लोगों A, B, C के पास कुल 360 रुपय है| A आधे रूपये B को देता हैऔर C अपने आधे A रूपये को सोंपता है | पैसे आपस में बदलने के बाद तीनो के पास बराबर मूल्य है | B के पास शुरुआत में कितने रुपय थे?ARs 0BRs 180CRs 120DRs 240
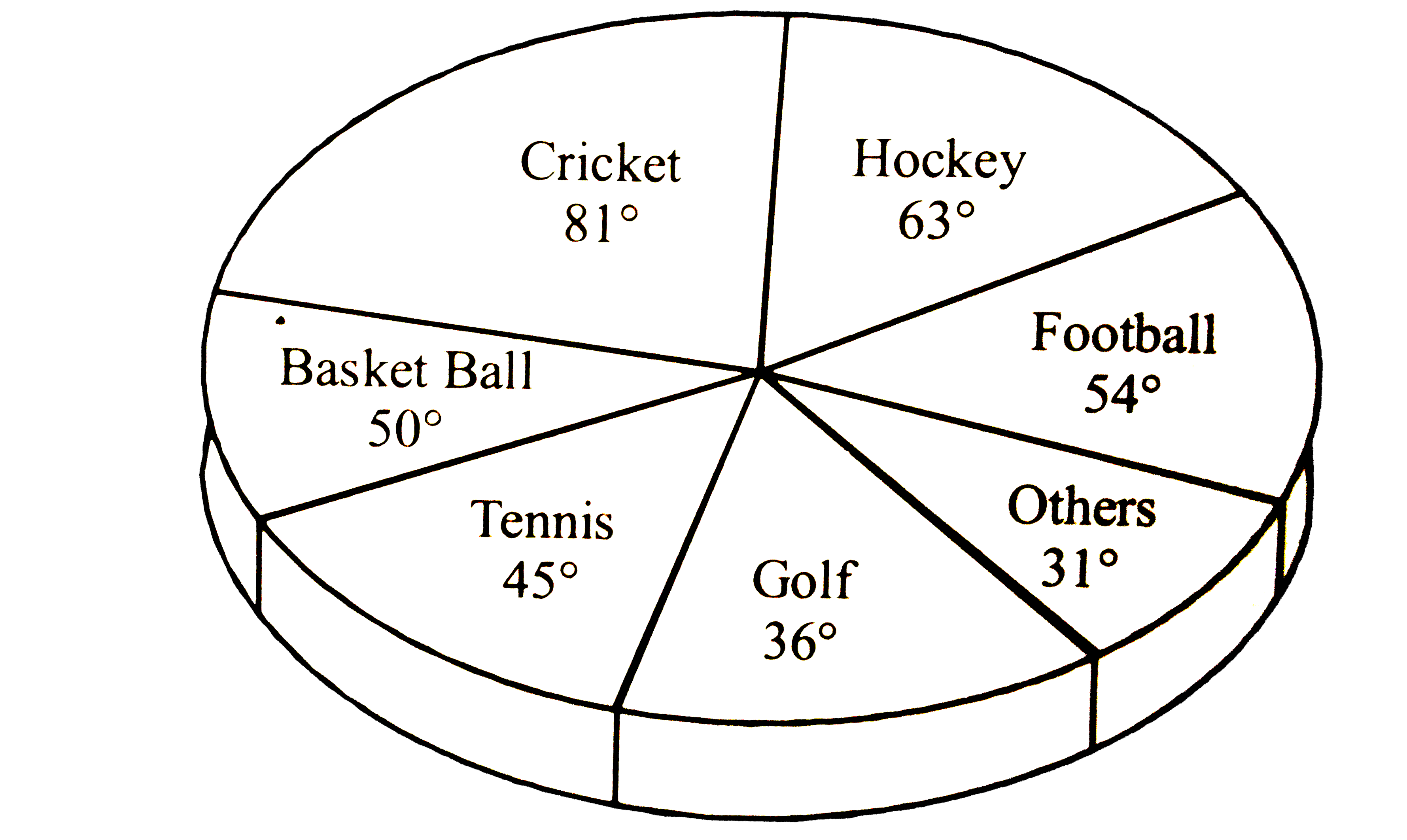
If the total amount spent on sports during the year was Rs. 2 crore, the amount spent on circket hockey together was
View SolutionX,Y and Z had taken adinner together. The cost of the meal of Z was 20% more than that of Y and the cost of the meal of X was 5/6 as much as the cost of the meal of Z. If Y paid X 100, then what was the total amount that all the three of them had paid?
View SolutionParmeshwarn invested an amount of Rs 12,000 at the rate of 10% per annum simple interest and another amount at the rate of 20% per annum of simple interest. The total interest earned at the end of one year on the total amount invested become 14% per annum. Find the total amount invested.
View SolutionNaveena spent 1,800 on a dress and 3,270 on books and notebooks. She still was left with 35% of the total amount she had originally. Find the total amount she had originally.
View SolutionRaj went to a market to buy a radio. But he had an amount which is equal to [1528] of the cost of the radio. If the cost of the raio is Rs. 560 then find the amount with him
View Solution