A shot is fired from the top of a tower at an angle $30^{\circ}$ to the horizontal with a velocity $v_{0}$ . If the height of the tower is h, calculate the speed of the shot at an altitude $h / 2$ , by energy methods.

Text Solution

Verified by Experts

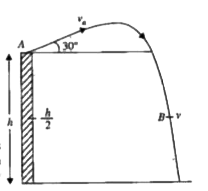
Total energy of the shot at A= Total energy of the shot at B
Let the velocity of the shot at an altitude $h / 2$ be v
$\frac{1}{2} m v_{0}^{2} + m g h = \frac{1}{2} m v^{2} + m \frac{g (h)}{2}$
$v^{2} = v_{0}^{2} + 2 g h - g h$
$v = \sqrt{v_{0}^{2} + g h}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
At a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is $30^{\circ}$ The height of the tower is
A $20 \sqrt{3} m$
B $\frac{20}{\sqrt{3}} m$
C $\frac{\sqrt{3}}{20 m}$
DNone of these
Question 2 - Select One
The angle of elevation of the top of a tower at a horizontal distance equal to the height of the tower from the base of the tower is
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
Dany acute angle
Question 3 - Select One
At a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is $30^{\circ}$ The height of the tower is
A $20 \sqrt{3} m$
B $\frac{20}{\sqrt{3}} m$
C $\frac{\sqrt{3}}{20} m$
DNone of these

ICSE-DYNAMICS-SHORT ANSWER QUESTIONS WITH ANSWERS

Home
Ask Doubt
Profile