An iron ball of mass 50 kg initially at rest at the top of an incline 4.5 m high and 10 m long is allowed to slide down the hill. Calculate the speed attained by the sphere at the bottom of the plane if the average retarding force due to friction is 20 kg wt.
mgh=(1/2)mv2+F×x
50×9.8×4.5=(1/2)×50×v2+20×9.8×10
v=3.13m/s.
Topper's Solved these Questions
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERES
43 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - VERY SHORT ANSWER QUESTIONS
60 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
Similar Questions
A solid cylinder 30 cm in diameter at the top of an inclined plane 2.0 m high is released and rolls down the incline without loss of energy due to friction. Its linear speed at the bottom is
View SolutionA skier starts from the top of a hill with speed 5m/s and slides down the hill of vertical height 60 m as shown. Neglect friction. Find his speed at the bottom.

View Solution
Knowledge Check
A solid cylinder 30 cm in diameter at the top of an inclined plane 2.0 m high is released and rolls down the incline without loss of energy due to friction. Its linear speed at the bottom is
A5.29 m/secB41 m/secC51 m/secD51 cm/secA body of mass 0.5 kg is taken up an inclined plane of length 10 m and height 5 m and then allowed to slide down to the bottom again. The coefficient of friction between the body and the plane is 0.1. The work done by the frictional force over the round trip is
A5 JB5√3JC−5JD−5√3JA solid sphere at the top of an inclined plane 0.6 m high is released and rolls down the incline without slipping and without loss of energy due to friction. Its linear speed at the bottom is about
A2.9m/sB2.42m/sC3.87m/sD1.53m/s
The power of a car is 20 hp . The car is facing resistance of 10 kg wt . Due to air and friction . Calculate the maximum speed attained by the car against this resistance .
View SolutionA block is placed on the top of a plane inclined at 37∘ with horizontal. The length of the plane is 5m. The block slides down the plane and reaches the bottom.
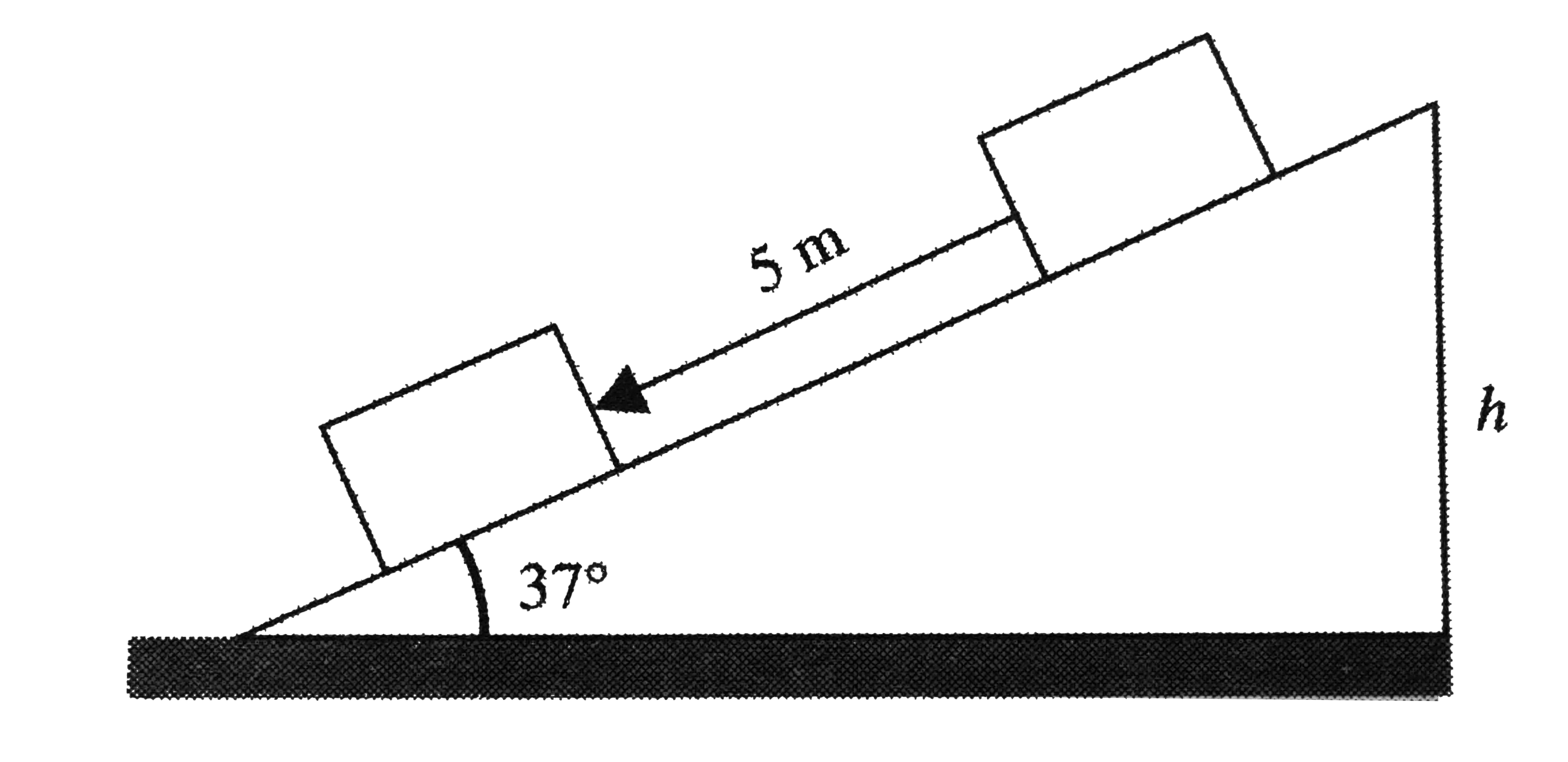
a. Find the speed of the block at the bottom if the inclined plane is smooth.
b. Find the speed of the block at the bottom if the coefficient of friction is 0.25.
View SolutionA block is placed on the top of a plane inclined at 37∘ with horizontal. The length of the plane is 5m. The block slides down the plane and reaches the bottom.

a. Find the speed of the block at the bottom if the inclined plane is smooth.
b. Find the speed of the block at the bottom if the coefficient of friction is 0.25.
View SolutionA block mass 3 kg slides down a frictionless inclined plane of length 6 m and height 4 m. if the block is released from rest at the top of the incline, what is its speed at the bottom?
View SolutionA box of mass 25kg starts from rest and slide down as inclined plane 8 metre long and 5 meter length . It is found to move at the bottom at 7m/s. What is the force of friction?
View Solution
