x+y≥3,7x+6y≤42,x≤5,y≤4,x,y>0
Text Solution
The correct Answer is:4x+9y−36≤0,3x+y−6≥0,x+3y−6≥0,4x−3y−12≤0
|
Topper's Solved these Questions
- INEQUALITIESBOOK - ICSECHAPTER - INEQUALITIESEXERCISE - EXERCISE 11 (c )
20 Videos
- INEQUALITIESBOOK - ICSECHAPTER - INEQUALITIESEXERCISE - CHAPTER TEST
4 Videos
- INEQUALITIESBOOK - ICSECHAPTER - INEQUALITIESEXERCISE - EXERCISE 11 (a)
32 Videos
- INDEX NUMBERS AND MOVING AVERAGES BOOK - ICSECHAPTER - INDEX NUMBERS AND MOVING AVERAGES EXERCISE - MULTIPLE CHOICE QUESTIONS
10 Videos
- INTRODUCTION TO THREE DIMENSIONAL GEOMETRYBOOK - ICSECHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS
17 Videos
Similar Questions
Knowledge Check
The objective function z=4x+3y subject to 3x+4y≤24,8x+6y≤48,x≤5,y≤6,x≥0,y≥0 can be maximized
Aat only one pointBat two points onlyCat infinite number of pointsDat three points onlyThe lines 5x+4y≥20,x≤6,y≤4,x≥0,y≥0 form
Aa squareBa rhombusCa triangleDa quadrilateralShaded, region of the constraints x+y≥5,2x+3y≤18,4x+3y≤24,x≥0,y≥0 is
A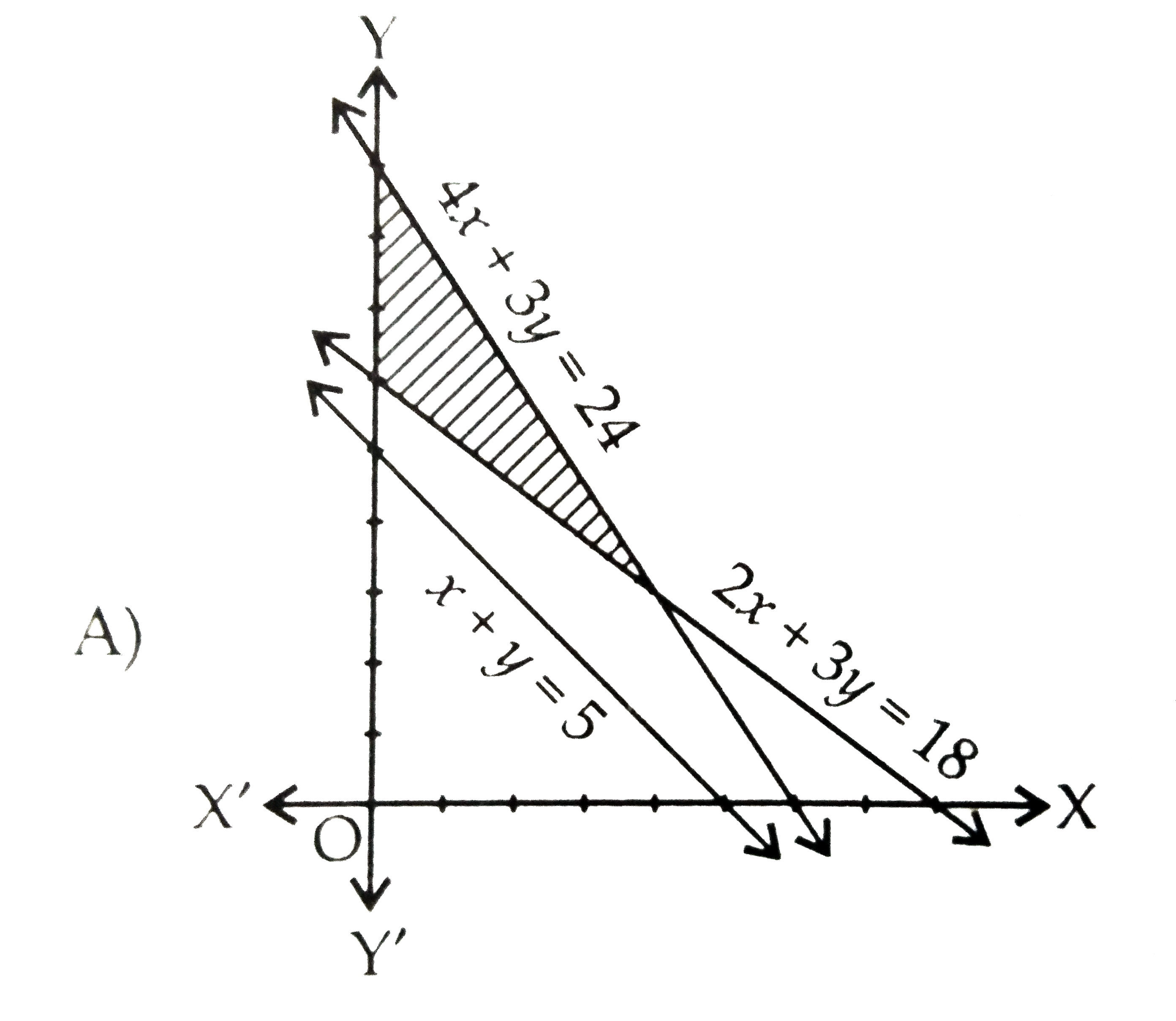 B
B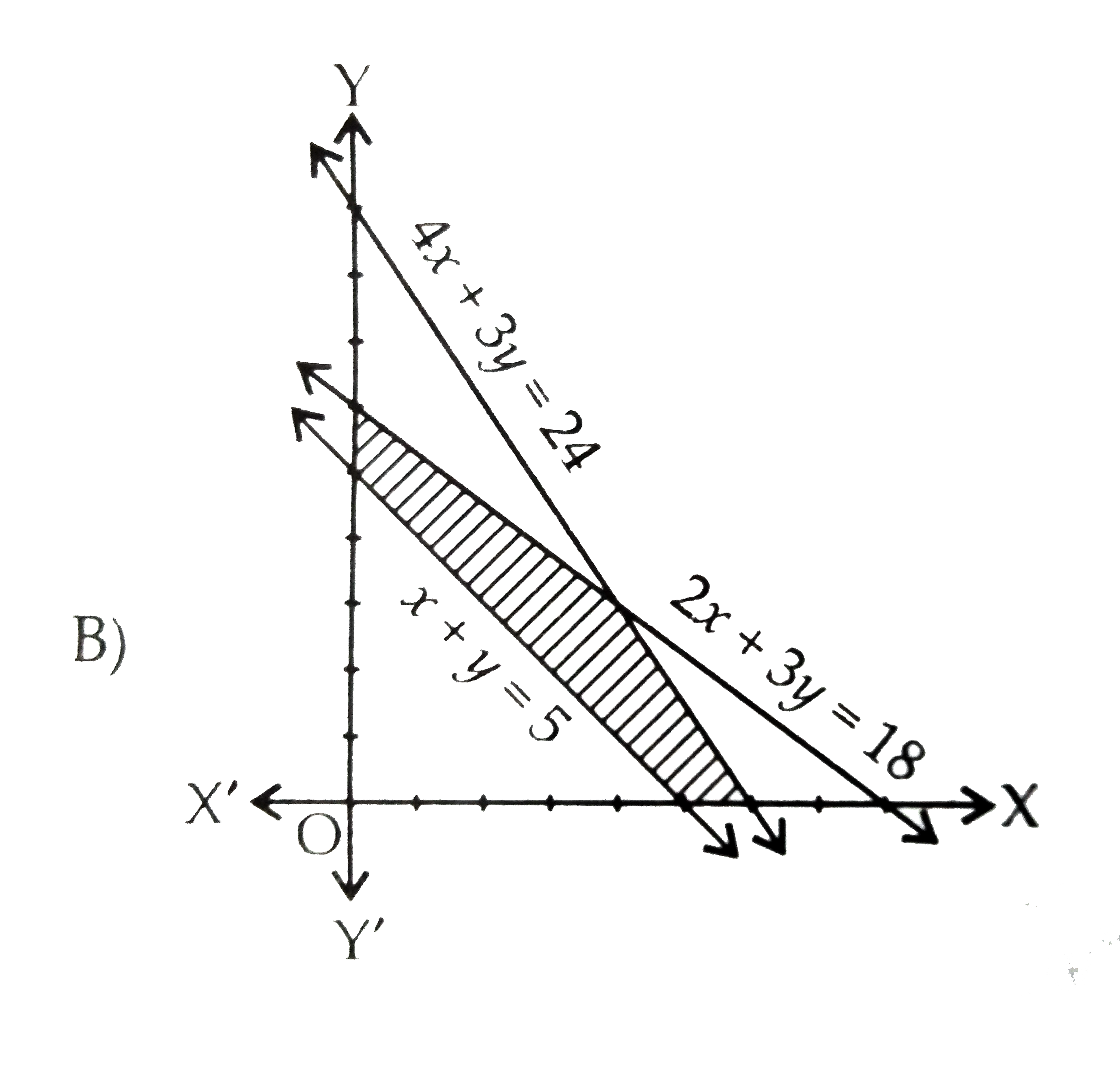 C
C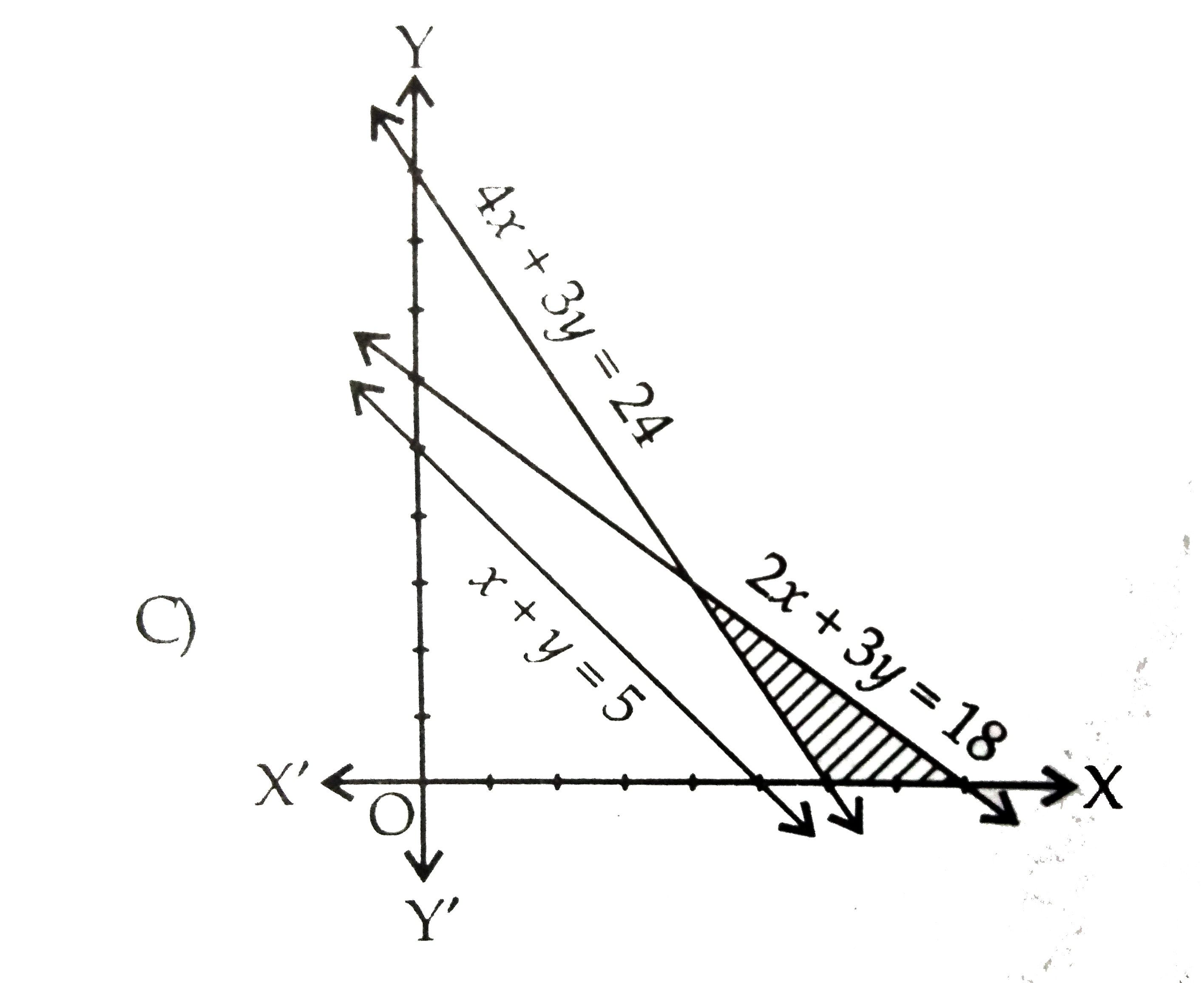 D
D
The maximum value of Z=5x+4y, subject to y≤2x,x≤2y,x+y≤3,x≥0,y≥0 is . . .
View SolutionMax value of z equal 3x + 2y subject to x+y≤3,x≤2,−2x+y≤1,x≥0,y≥0 is
View SolutionThe maximum value of z=x+y subject to x+y≤10,3x−2y≤15,x≤6,x≥0,y≥0 is
View SolutionThe maximum value of z=6x+4y subject to x≤2,x+y≤3,−2x+y≤1,x≥0,y≥0, is
View SolutionThe objective function z=x+y subject to x+y≤10,3x−2y≤15,x≤6,x≥0,y≥0 can be maximized
View Solution
