In Fig. A and B represent two straight wires carrying equal currents in a direction normal to the plane of paper inwards.
×⋅×AKBFig.10.11
What will be the magnetic field at the mid point K of the line joining A and B. Give reason.
The net magnetic field at the point K is zero.
Reason: The point K is equidistant from the wires A and B, and the wires A and B carry equal currents, so the magnetic fields at the point K due to current in the wires A and B are equal in magnitude, but opposite in direction. Due to current in the wire A. it is downwards in the plane of paper, while due to current in the wire B, it is upwards in the plane of paper. The two fields cancel each other.
Topper's Solved these Questions
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10(A)
28 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10(B)
12 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C) NUMERICALS
35 Videos
- FORCE BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1( C) Multiple Choice questions
2 Videos
Similar Questions
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionTwo similar coaxial coils, separated by some distance, carry the same current I but in opposite directions. The magnitude of the magnetic field B at a point on the axis at the mid point of the line joining the centre is :
View Solution
Knowledge Check
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
Aμ0idπ(d2+x2)Bμ0ixπ(d2−x2)Cμ0ix(d2+x2)Dμ0id(d2+x2)Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
Aμ0idπ(d2+x2)Bμ0ixπ(d2−x2)Cμ0ix(d2+x2)Dμ0id(d2+x2)Two infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
ATwice the magnetic field produced due to each of the wiresBHalf of the magnetic field produced due to each of the wiresCSquare of the magnetic field produced due to each of the wiresDZero
A straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.

View SolutionTwo long straight parallel wieres are 2m apart, perpendicular to the plane of the paper. The wire A carries a current of 9.6A, directed into the plane of the paper. The wire B carries a current such that the magnetic field of induction at the point P, at a distance of 1011 m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont S.
c. the force per unit length on the wire B.
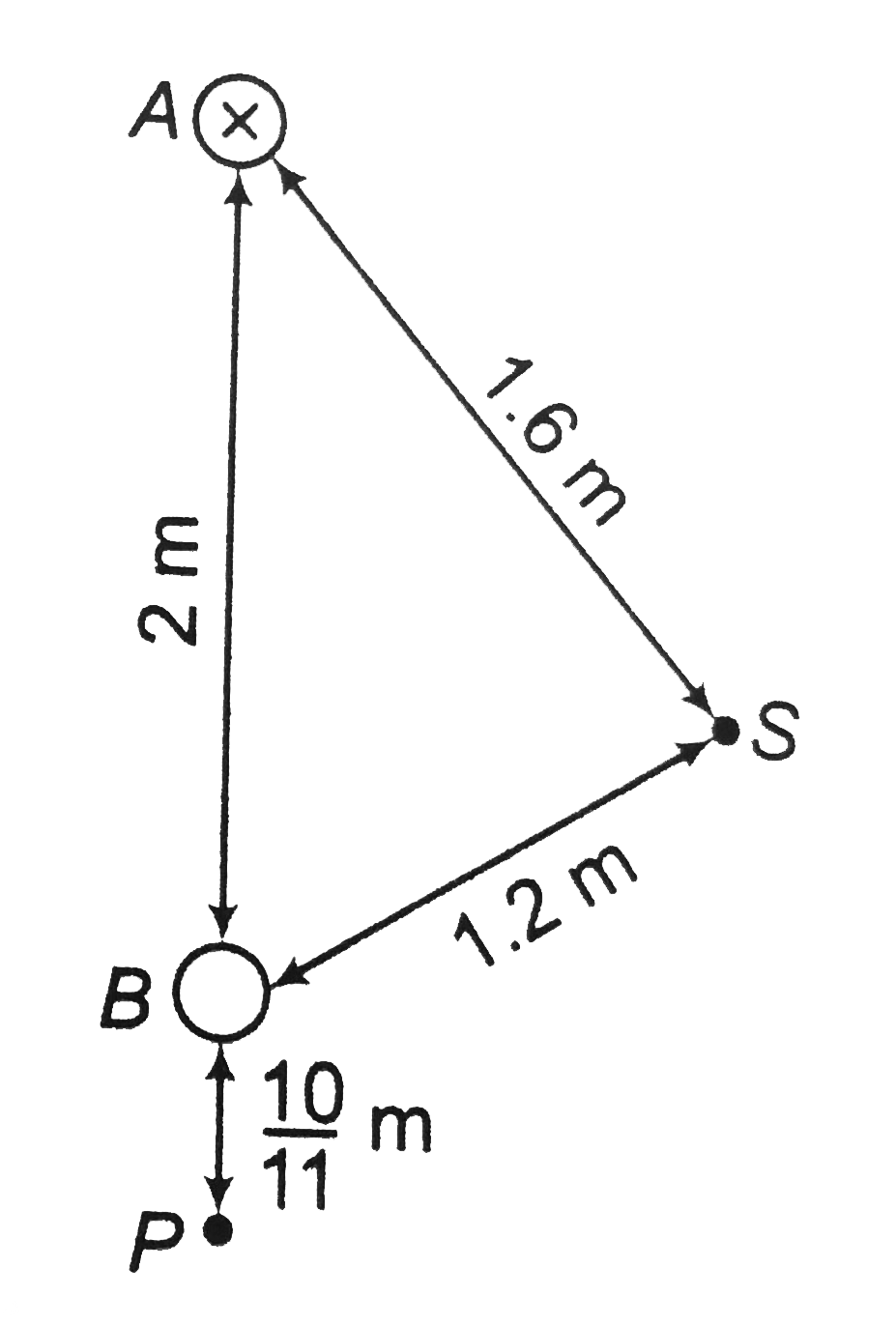
View SolutionTwo long straight parallel wieres are 2m apart, perpendicular to the plane of the paper. The wire A carries a current of 9.6A, directed into the plane of the paper. The wire B carries a current such that the magnetic field of induction at the point P, at a distance of 1011 m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont S.
c. the force per unit length on the wire B.

View SolutionAssertion Two infinitely long wires A and B carry unequal currents both in inward direction.

Then, there is only point (excluding the ponts at infinity), where net magnetic field is zero.
Reason That point lies between points A and B.
View SolutionTwo similar coaxial coils, separated by some distance, carry the same current I but in opposite directions. The magnitude of the magnetic field B at a point on the axis at the mid point of the line joining the centre is :
View Solution
