Line segments AB||PQ. Also, AO=OQ=3 cm Establish congruency between △AOB and △QOP .
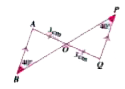
The correct Answer is:ΔAOB≅ΔQO;ASA
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLESBOOK - ICSECHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - Try this
12 Videos
- CONGRUENCE OF TRIANGLESBOOK - ICSECHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - EXERCISE 13.2
11 Videos
- CONGRUENCEBOOK - ICSECHAPTER - CONGRUENCEEXERCISE - EXERCISE 21
23 Videos
- CONSTRUCTION BOOK - ICSECHAPTER - CONSTRUCTION EXERCISE - EXERCISE
18 Videos
Similar Questions
Draw a line segment AB=7.6cm. without constructing parallel lines at A and B, find three points P,QandR on ¯¯¯¯¯¯AB such that ¯¯¯¯¯¯AP=¯¯¯¯¯¯PQ=¯¯¯¯¯¯QR=¯¯¯¯¯¯RB.
View SolutionDraw a line segment AB. Find a point P, 4 cm above the line segment, and draw a line segment parallel to AB through P.
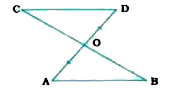
View SolutionLine segment AB is parallel to another line segment CD. O is the midpoint of AD (see the given figure). Show that
(i) △AOB=△DOC
(ii) O is also the midpoint of BC
View SolutionDraw a line segment AB of length 5.3 cm. using two different methods bisect AB.
View SolutionDraw line segment PQ with the length 9cm.
View SolutionDraw a line segment AB of 4cm in length . Draw a line perpendicular to AB through A and B, respectively. Are these lines parallel?
View SolutionDraw a line segment AB = 4 cm . Now construct another line segment PQ such that PQ is thrice the length of AB. Verify your construction by measuring PQ with a ruler.
View SolutionConstruct a line segment AB = 8.9 cm. Construct another segment AC such that C lies on AB and AC = 3.8 cm. Measure the length of the remaining line segment.
View SolutionDraw a line segment PQ = 8 cm. Using ruler and compass, obtain a line segment of length 34(PQ).
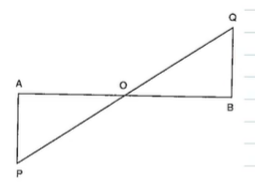
View SolutionIn Figure, AP and BQ are perpendiculars to the line segment AB and AP=BQ. Prove that O is the mid-point of line segment AB and PQ.
View Solution
