If in applying the quadratic formula to a quadratic equation f(x)=ax2+bx+c=0 it happens that c=b24a Then the graph of y = f (x) will certainly
A
have a maximum
B
have a minimum
C
be a tangent to x-axis
D
be a tangent to the y-axis
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- QUADRATIC AND CUBIC EQUATIONSBOOK - DISHA PUBLICATIONCHAPTER - QUADRATIC AND CUBIC EQUATIONSEXERCISE - Standard Level
37 Videos
- QUADRATIC AND CUBIC EQUATIONSBOOK - DISHA PUBLICATIONCHAPTER - QUADRATIC AND CUBIC EQUATIONSEXERCISE - Expert Level
17 Videos
- QUADRATIC AND CUBIC EQUATIONSBOOK - DISHA PUBLICATIONCHAPTER - QUADRATIC AND CUBIC EQUATIONSEXERCISE - Test Yourself
15 Videos
- PROGRESSIONSBOOK - DISHA PUBLICATIONCHAPTER - PROGRESSIONSEXERCISE - TEST YOURSELF
15 Videos
- RATIO,PROPORTION AND VARIATIONBOOK - DISHA PUBLICATIONCHAPTER - RATIO,PROPORTION AND VARIATIONEXERCISE - Test Yourself
15 Videos
Similar Questions
Knowledge Check
In quadratic equation ax2+bx+c=0, if discriminant D=b2−4ac, then roots of quadratic equation are:
Areal and distinct, if D>0Breal and equal (repeated roots), if D=0Cnon-real (imaginary), if D<0DNone of the aboveIf in the quadratic function f(x)=ax2+bx+c, a and c are both negative constant, which of the following could be the graph of function f?
A B
B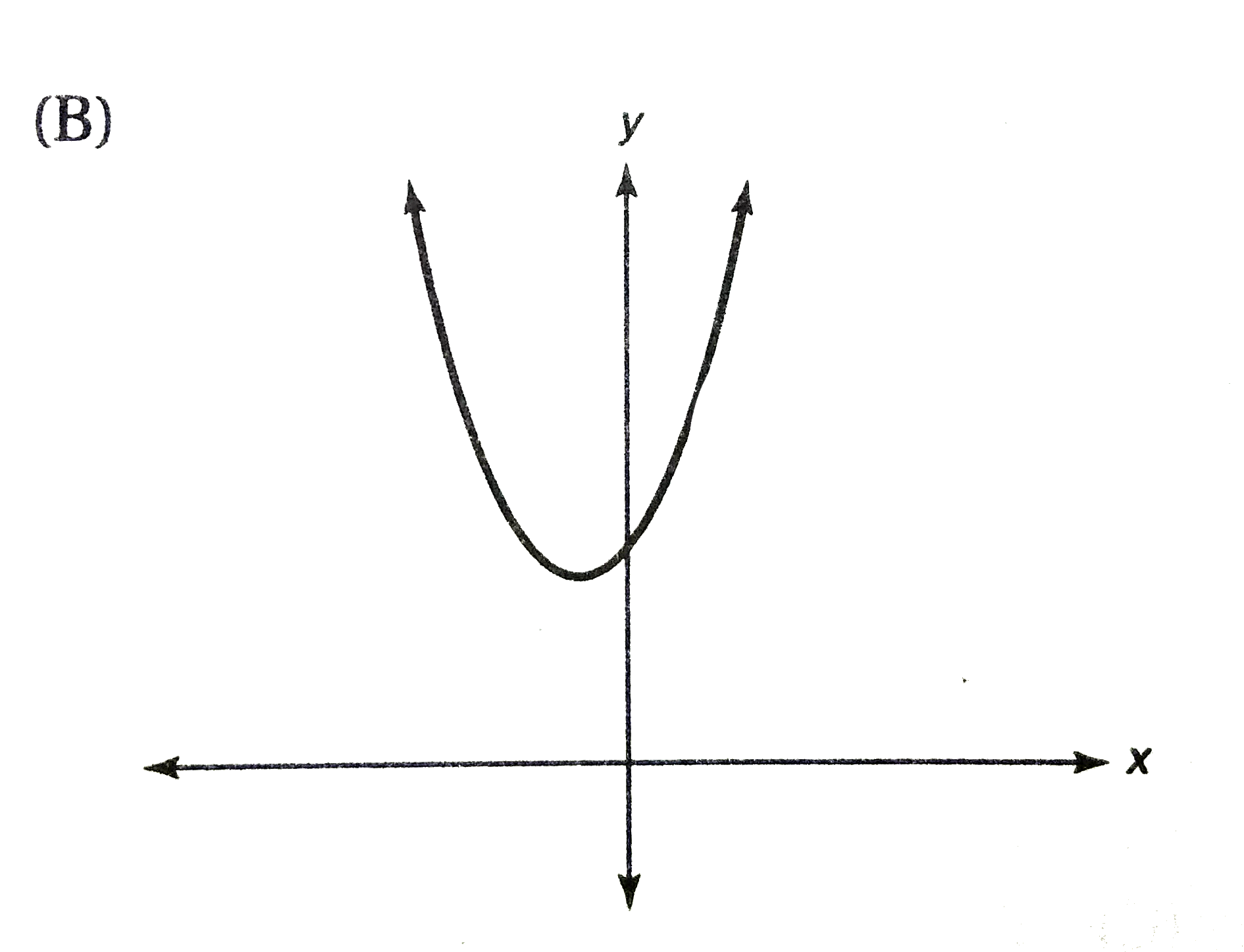 C
C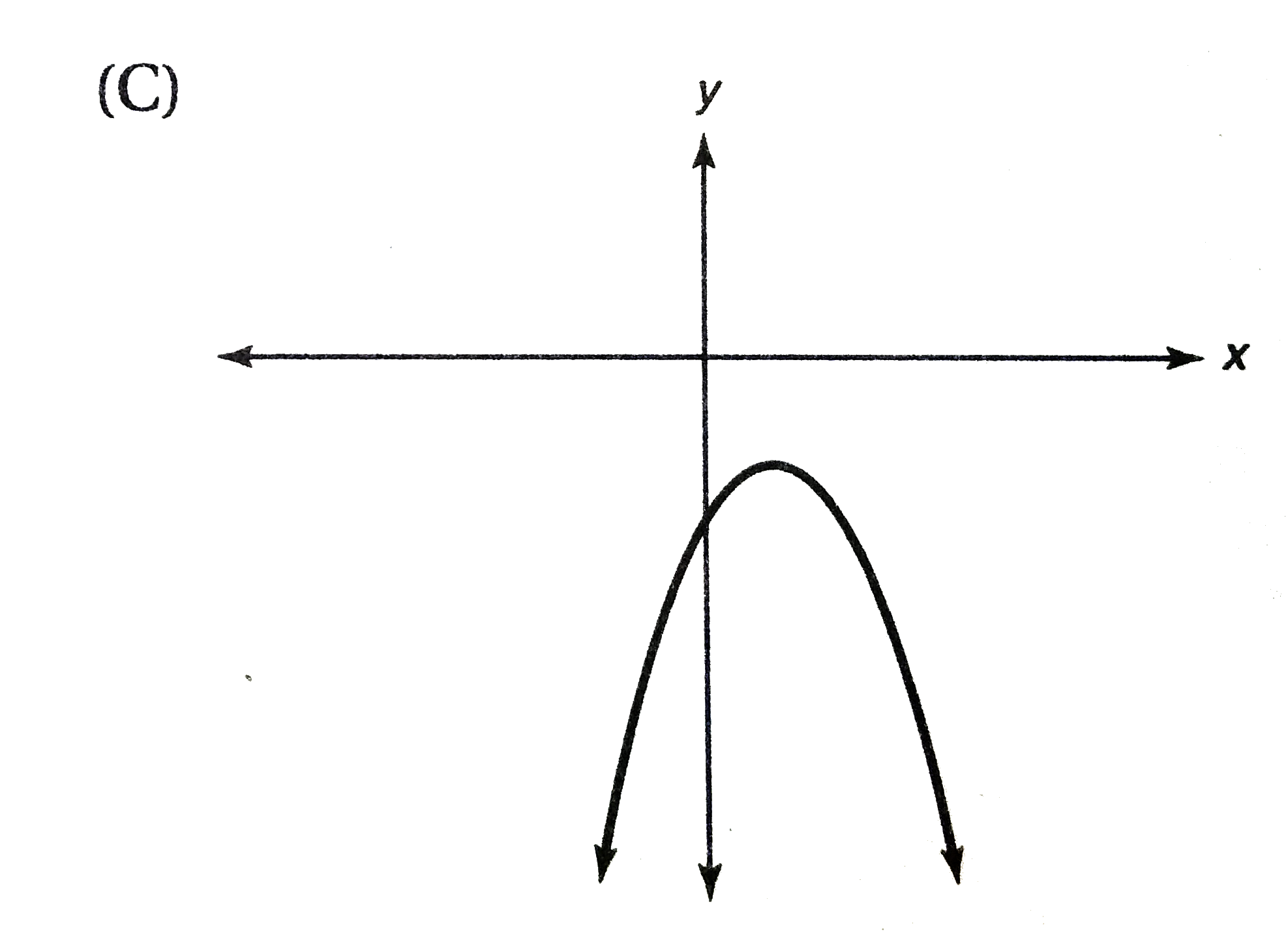 D
D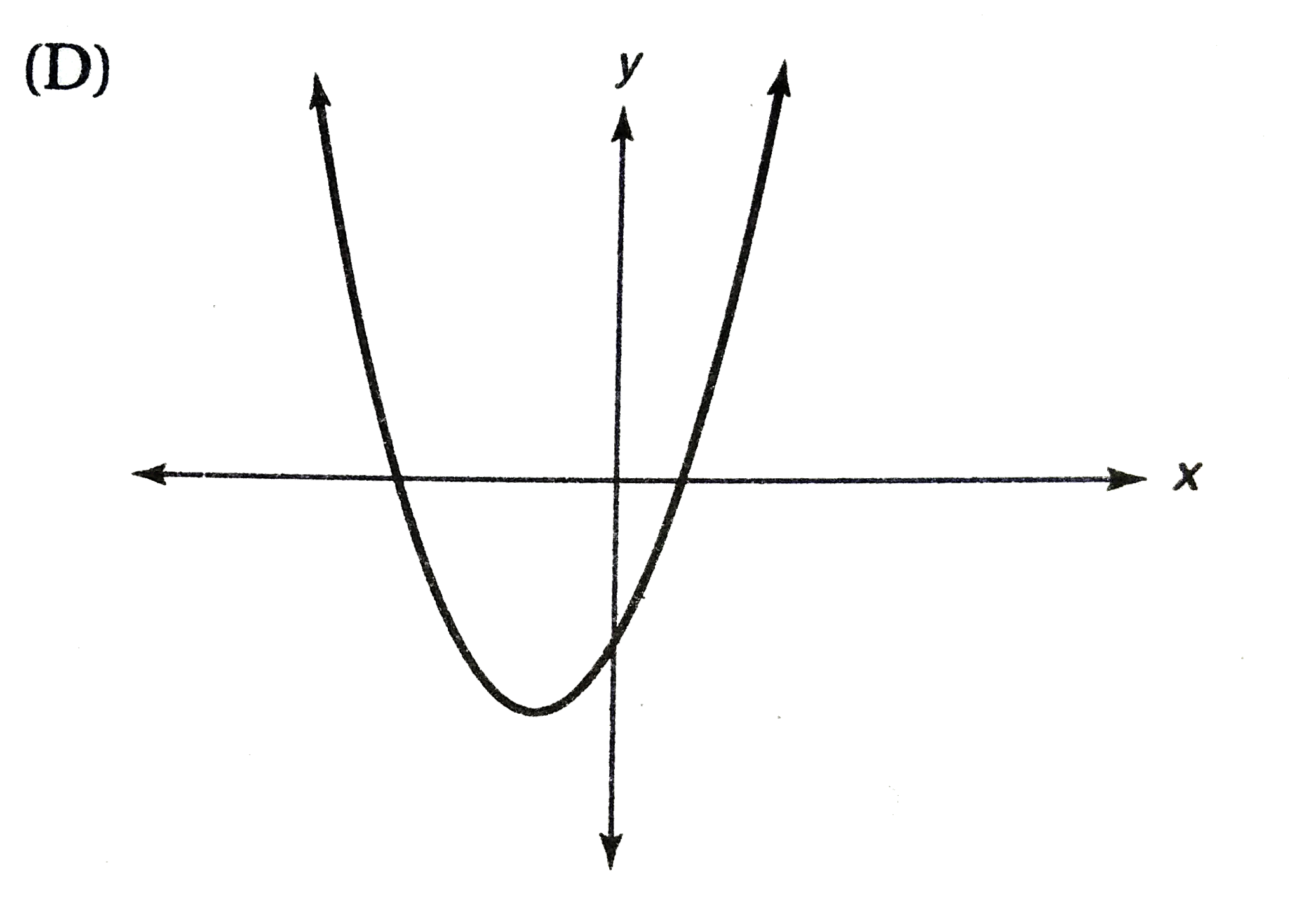
The graph of quadratic polynomical f(x)=ax2+bx+c is shown below
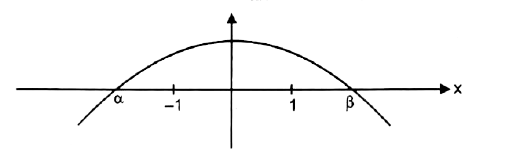
View SolutionIf x=1 is a solution of the quadratic equation ax2−bx+c=0, then b is equal to _______.
View SolutionWrite the quadratic equation 7=4x−x2 in the form of ax2+bx+c=0
View SolutionGraph of quadratic expression y=ax2+bx+c is given then
View SolutionIn quadratic equation ax2+bx+c=0, if discriminant D=b2−4ac, then roots of quadratic equation are:
View Solutionif α&βare the roots of the quadratic equation ax2+bx+c=0, then the quadratic equation ax2−bx(x−1)+c(x−1)2=0 has roots
View Solution
