बायो सेवर्ट नियम का उल्लेख कीजिये। सेमी त्रिज्या के वृत्ताकार लूप में एम्पियर की धारा बह रही है। लूप के केंद्र पर चुम्बकीय क्षेत्र की गणना कीजिये।
B=3.14×10−5 Tesla
Topper's Solved these Questions
- इंटरमीडिएट परीक्षा 2018 BOOK - UP BOARD PREVIOUS YEARCHAPTER - इंटरमीडिएट परीक्षा 2018 EXERCISE - भौतिक विज्ञान 373 (FU)
28 Videos
- इंटरमीडिएट परीक्षा 2018 BOOK - UP BOARD PREVIOUS YEARCHAPTER - इंटरमीडिएट परीक्षा 2018 EXERCISE - भौतिक विज्ञान 372 (FO)
28 Videos
- इंटरमीडिएट परीक्षा 2018 BOOK - UP BOARD PREVIOUS YEARCHAPTER - इंटरमीडिएट परीक्षा 2018 EXERCISE - भौतिक विज्ञान 373 (FT)
28 Videos
- अर्द्धचालक इलेक्ट्रॉनिकी पदार्थ , युक्तियाँ तथा सरल परिपथ BOOK - UP BOARD PREVIOUS YEARCHAPTER - अर्द्धचालक इलेक्ट्रॉनिकी पदार्थ , युक्तियाँ तथा सरल परिपथ EXERCISE - विस्तृत उत्तीय प्रश्नोत्तर ?
52 Videos
- इण्टरमीडिएट परीक्षा, 2013BOOK - UP BOARD PREVIOUS YEARCHAPTER - इण्टरमीडिएट परीक्षा, 2013EXERCISE - भौतिक विज्ञान - द्वितीय प्रश्न - पत्र (373(IH))
23 Videos
Similar Questions
1- kHz आवृत्ति तथा 10 V शिखर वोल्टता के सन्देश सिग्नल का उपयोग किसी 1 MHz आवृत्ति तथा 20 V शिखर वोल्टा की वाहक तरंगो को मॉडुलित करने में किया गया है। उत्पन्न पार्श्व बेंड की आवृत्तियाँ होगी -
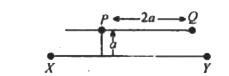
View Solutionदिए गए चित्र में XY एक अनंत रेखीय आवेश वितरण है। बिंदु P तथा Q चित्र में दिखाया गया है। बिंदु P तथा Q पर वैद्युत क्षेत्र की तीव्रताओं का अनुपात है -
View Solutionव्योम तरंगो द्वारा क्षैतिज से पार संचार के लिए संचार के लिए निम्न में से कौन - सी आवृत्ति उपयुक्त होगी ?
View Solutionऊर्जा बैण्ड के आधार पर चालक,अचालक एवं अर्द्धचालकों का वर्गीकरण स्पष्ट कीजिए।
View Solutionवैद्युत क्षेत्र की तीव्रता का मात्रक है
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण अक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण निरक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View Solutionबायो सेवर्ट का नियम तथा एम्पियर का नियम (part 1)
View Solutionबायो सेवर्ट का नियम तथा एम्पियर का नियम (part 2)
View Solutionधारावाही वृत्ताकार लूप और कुंडली के केंद्र पर चुंबकीय क्षेत्र
View Solutionधारावाहिक चाप के कारण चुंबकीय क्षेत्र|वृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionबायो सेवर्ट का नियम
View Solutionधारावाही वृत्ताकार लूप और कुंडली के अक्ष पर चुंबकीय क्षेत्र
View SolutionRecap|धारावाही लूप के कारण चुम्ब्कीय क्षेत्र
View Solutionबायो सेवर्ट नियम के अनुप्रयोग
View Solution
