Two vectors →A and →B of magnitude 5 units and 7 units respectively make an angle 60∘ with each other as shown below. Find the magnitude of the resultant vector and its direction with respect to the vector G →A.
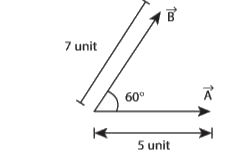
By following the law of triangular addition, the resultant vector is given by
→R=→A+→B
as illustrated below

Th e magnitude of the resultant vector →R is given by
R=∣∣→R∣∣=√52+72+2×5×7cos60∘
R=√25+49+70×12=√109 units
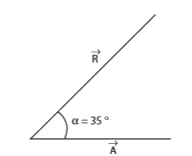
The angle α between →R and →A is given by
tanα=BsinθA+Bcosθ
tanα=7×sin605+7cos60=7√310+7=7√317≅0.713
∴a≅35∘
Topper's Solved these Questions
- KINEMATICSBOOK - NCERT TAMILCHAPTER - KINEMATICSEXERCISE - EXERCISE (I. Multi Choice Question)
15 Videos
- KINEMATICSBOOK - NCERT TAMILCHAPTER - KINEMATICSEXERCISE - EXERCISE (IV. Exercises )
20 Videos
- HEAT AND THERMODYNAMICSBOOK - NCERT TAMILCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - EVALUATION (Numerical Problems)
13 Videos
- KINETIC THEORYBOOK - NCERT TAMILCHAPTER - KINETIC THEORYEXERCISE - ADDITIONAL EXERCISE
4 Videos
Similar Questions
Two vectors of 10 units & 5 units make an angle of 120∘ with each other.Find the magnitude & angle of resultant with vector of 10 unit magnitude.
View SolutionTwo vectors have magnitudes 6 and 8 units, respectively. Find the magnitude of the resultant vector if the angle between vectors is (a) 60∘ (b) 90∘ and ( c ) 120∘.
View Solution
Knowledge Check
When two vectors →A and →B of magnitudes a and b respectively are added, the magnitude of resultant vector is always
AEqual to (a+b)BLess than (a+b)CGreater than (a+b)DNot greater than (a+b)The angle between two vectors →a and →b with magnitudes √3 and 4, respectively and →a.→b=2√3 is:
Aπ6Bπ3Cπ2D5π2Two vectors →A and →B have magnitude in the ratio 1:2 respectively. Their difference vector has as magnitude of 10 units, and the angle between →A&→B is 120∘ . The magnitude of →Aand→B are :
A5√7,10√7B5√3,10√3C10√7,20√7D10√3,20√3
Two vectors have magnitudes 6 and 8 units, respectively. Find the magnitude of the resultant vector if the angle between vectors is (a) 60∘ (b) 90∘ and ( c ) 120∘.
View SolutionTwo vectors →A and →B have magnitude in the ratio 1:2 respectively. Their difference vector has as magnitude of 10 units, and the angle between →A&→B is 120∘ . The magnitude of →Aand→B are :
View SolutionThe magnitudes of vectors →A,→Band→C are 3,4 and 5 units respectively. If →A+→B=→C, the angle between →A and vecB is
View SolutionThe vectors →A has a magnitude of 5 unit →B has a magnitude of 6 unit and the cross product of →Aand→B has a magnitude of 15 unit. Find the angle between →Aand→B.
View SolutionThe magnitudes of vectors →A,→Band→C are 3,4 and 5 units respectively. If →A+→B=→C, the angle between →A and →B is
View Solution
