In the cricket game, a batsman strikes the ball such that it moves with the speed $30 m s^{- 1}$ at an angle $30^{\circ}$ with the horizontal as shown in the figure. The boundary line of the cricket ground is located at a distance of 75 m from the batsman? Will the ball go for a six? (Neglect the air resistance and take acceleration due to gravity $g = 10 m s^{- 2}$ ).

Text Solution

Verified by Experts

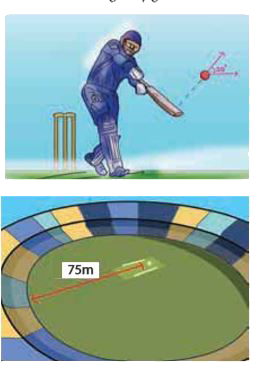
The motion of the cricket ball in air is essentially a projectile motion. As we have already seen, the range (horizontal distance) of the projectile motion is given by
$R = \frac{u^{2} sin 2 θ}{g}$
The initial speed $u = 30 m s^{- 1}$
The projection angle $θ = 30^{\circ}$
The horizontal distance travelled by the cricket ball
$R = \frac{{(30)}^{2} \times {sin 60}^{\circ}}{10} = \frac{900 \times \frac{\sqrt{3}}{2}}{10} = 77.94 m$
This distance is greater than the distance of the boundary line. Hence the ball will cross this line and go for a six.

Updated on:21/07/2023