If AD is a median of a ΔABC and P is a point on AC such that ar(ΔADP) : ar (ΔABD) = 2:3, then ar (ΔPDC) : ar (ΔABC) is .
1:6
1:5
2:5
3:5
The correct Answer is:A
To solve the problem, we will follow these steps:
1. Understand the Given Information: We have triangle ABC with AD as a median. This means D is the midpoint of BC. We also know that the area of triangle ADP is in the ratio of 2:3 with the area of triangle ABD.
2. Assign Variables: Let's denote the area of triangle ABD as X. Since D is the midpoint, the area of triangle ACD will also be X.
3. Calculate the Area of Triangle ADP: Given that the area of triangle ADP to the area of triangle ABD is 2:3, we can express the area of triangle ADP as:
Area of △ADP=23×X=2X3
4. Calculate the Area of Triangle ADC: The area of triangle ADC is equal to the area of triangle ABD, which we have already defined as X.
5. Find the Area of Triangle PDC: To find the area of triangle PDC, we can use the relationship:
Area of △ADC=Area of △ADP+Area of △PDC
Therefore, we can express the area of triangle PDC as:
Area of △PDC=Area of △ADC−Area of △ADP
Substituting the values we have:
Area of △PDC=X−2X3=3X3−2X3=X3
6. Calculate the Area of Triangle ABC: The area of triangle ABC is the sum of the areas of triangles ABD and ACD:
Area of △ABC=Area of △ABD+Area of △ACD=X+X=2X
7. Find the Ratio of Areas: Now we can find the ratio of the area of triangle PDC to the area of triangle ABC:
Ratio=Area of △PDCArea of △ABC=X32X=13×12=16
Thus, the final answer is:
ar(ΔPDC):ar(ΔABC)=1:6
Area of △ADP=23×X=2X3
Area of △ADC=Area of △ADP+Area of △PDC
Therefore, we can express the area of triangle PDC as:
Area of △PDC=Area of △ADC−Area of △ADP
Substituting the values we have:
Area of △PDC=X−2X3=3X3−2X3=X3
Area of △ABC=Area of △ABD+Area of △ACD=X+X=2X
Ratio=Area of △PDCArea of △ABC=X32X=13×12=16
ar(ΔPDC):ar(ΔABC)=1:6
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SOF INTERNATIONAL MATHEMATICS OLYMPIADEXERCISE - EVERYDAY MATHEMATICS10videos
SOF INTERNATIONAL MATHEMATICS OLYMPIAD
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SOF INTERNATIONAL MATHEMATICS OLYMPIADEXERCISE - ACHIEVERS SECTION5videos
SOF INTERNATIONAL MATHEMATICS OLYMPIAD
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SOF INTERNATIONAL MATHEMATICS OLYMPIADEXERCISE - ACHIEVERS SECTION5videos
SOF INTERNATIONAL MATHEMATICS OLYMPIAD
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - QUADRILATERALSEXERCISE - Achievers Section (HOTS)3videos
QUADRILATERALS
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - STATISTICSEXERCISE - Achievers Section (HOTS)3videos
STATISTICS
Similar Questions
In △ABC ,AD is a median and P is a point on AD such that AP : PD = 3 : 4. Then ar(△BPD):ar(△ABC) is equal to:
त्रिभुज ABC में, AD एक माध्यिका है और P, AB पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है| ar(△BPD):ar(△ABC) ज्ञात करें |View SolutionABC,DEAB=2:3 and ar(ΔDEF)=44sq.units then ar(ΔABC)is
View Solution
Knowledge Check
- Question 1 - Select One
In the given figure, AD is the median and E is any point on AC, such that ar(ΔMDE) : ar(ΔABD) = 2 : 3, then find the ratio of ar(ΔEDC): ar(ΔABC).
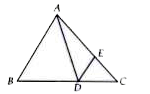 A3 : 4B1 : 6C6 : 1D4 : 3
A3 : 4B1 : 6C6 : 1D4 : 3 - Question 2 - Select One
It is given that ΔABC~ΔPRQandBCQR=23 then ar(ΔPQR)ar(ΔABC)=?
A23B32C49D94 - Question 3 - Select One
It is given that ΔABC−ΔPQR, with BCQR=14. Then arΔPQRarΔABC is equal to:
A16B3C13D19
In an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?
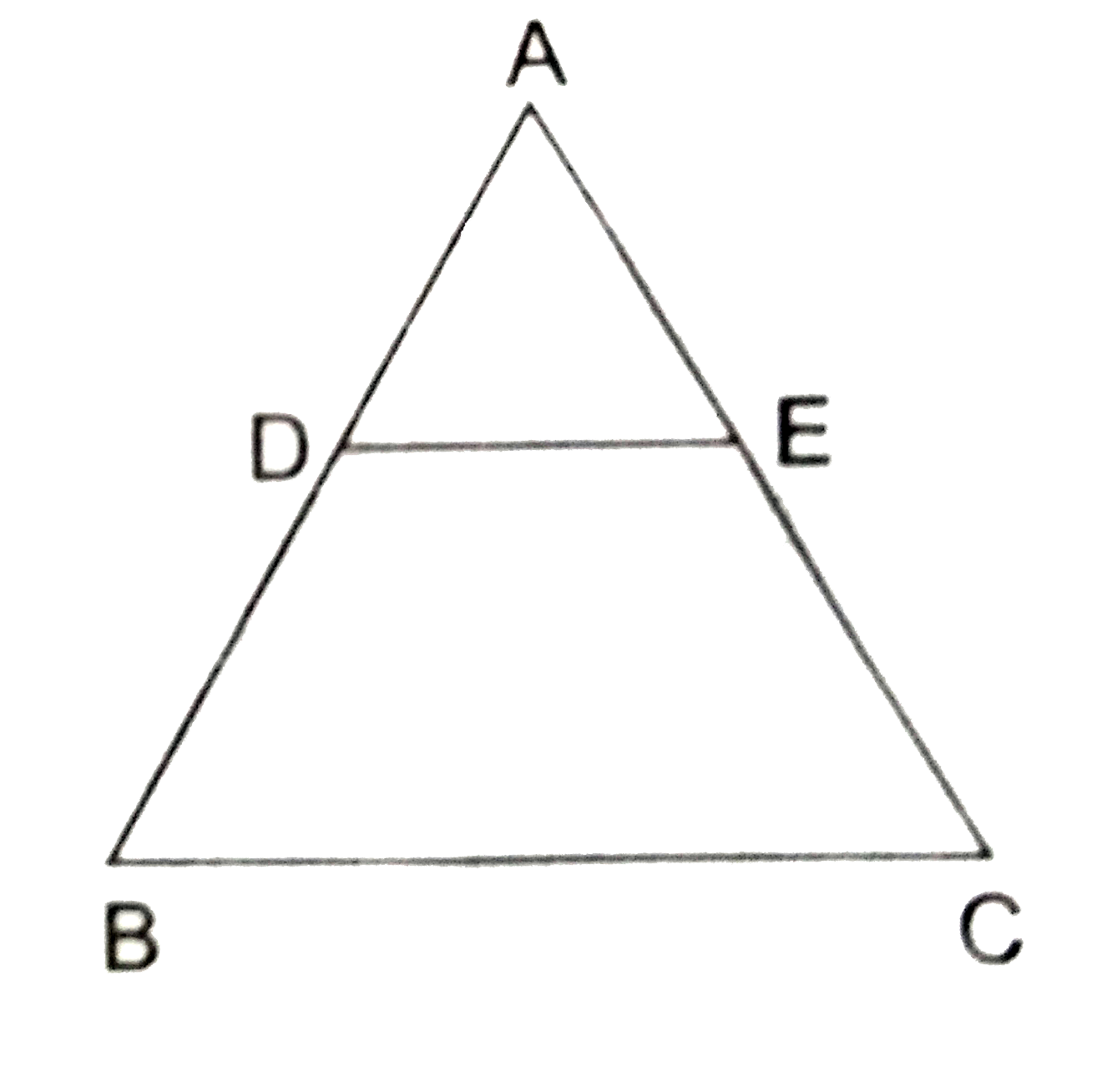 View Solution
View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).
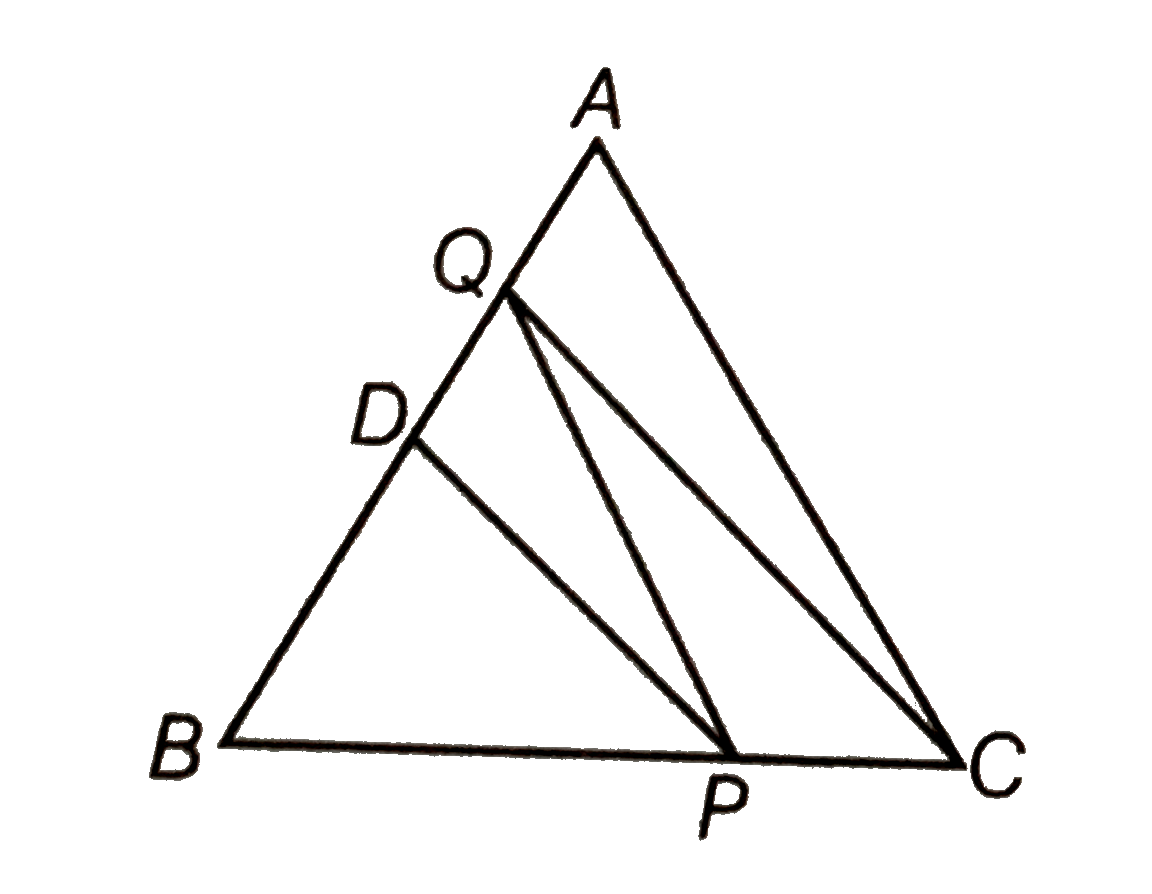 View Solution
View SolutionE is any point on median AD of ∠ABC .If ar(ΔABE)=10cm2 then ar(ΔACE) is
View SolutionIn △ABC, AD is median and P is the point on AD such that AP : PD = 3 : 4, then ar(△APB):ar(△ABC) is equal to :
त्रिभुज ABC में, AD मध्यिका है तथा P, AD पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है, तो ar(△APB):ar(△ABC) का मान किसके बराबर होगा ?View SolutionIn the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
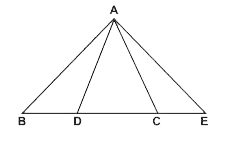 View Solution
View Solution

