The top of a broken tree has its top end touching the ground at a distance 15 m from the bottom, the angle made by the broken end with the ground is 30∘. Then length of broken part is
10 m
√3m
5√3m
10√3m
The correct Answer is:D
To find the length of the broken part of the tree, we can follow these steps:
Step 1: Understand the Geometry of the Problem
We have a broken tree represented as a right triangle. The point where the tree breaks is point A, the point where the tree touches the ground is point M, and the base of the tree is point B. The distance from point B to point M is given as 15 m, and the angle made by the broken part (AM) with the ground (BM) is 30 degrees.
Step 2: Identify the Right Triangle
In the right triangle ABM:
- AM is the hypotenuse (the length of the broken part).
- BM is the base (the distance from the bottom of the tree to the point where the top touches the ground), which is 15 m.
- Angle AMB is 30 degrees.
Step 3: Use Trigonometric Ratios
We can use the cosine function to relate the adjacent side (BM) and the hypotenuse (AM):
cos(θ)=AdjacentHypotenuse
Here, θ=30∘, the adjacent side is BM (15 m), and the hypotenuse is AM (which we want to find).
Step 4: Substitute Values into the Cosine Formula
cos(30∘)=BMAM
Substituting the known values:
cos(30∘)=15AM
We know that cos(30∘)=√32, so we can write:
√32=15AM
Step 5: Solve for AM
Cross-multiplying gives:
AM⋅√3=30
Now, divide both sides by √3:
AM=30√3=10√3 m
Conclusion
The length of the broken part of the tree is 10√3 meters.
---
We have a broken tree represented as a right triangle. The point where the tree breaks is point A, the point where the tree touches the ground is point M, and the base of the tree is point B. The distance from point B to point M is given as 15 m, and the angle made by the broken part (AM) with the ground (BM) is 30 degrees.
In the right triangle ABM:
- AM is the hypotenuse (the length of the broken part).
- BM is the base (the distance from the bottom of the tree to the point where the top touches the ground), which is 15 m.
- Angle AMB is 30 degrees.
We can use the cosine function to relate the adjacent side (BM) and the hypotenuse (AM):
cos(θ)=AdjacentHypotenuse
Here, θ=30∘, the adjacent side is BM (15 m), and the hypotenuse is AM (which we want to find).
cos(30∘)=BMAM
Substituting the known values:
cos(30∘)=15AM
We know that cos(30∘)=√32, so we can write:
√32=15AM
Cross-multiplying gives:
AM⋅√3=30
Now, divide both sides by √3:
AM=30√3=10√3 m
The length of the broken part of the tree is 10√3 meters.
Similar Questions
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is
View SolutionA telegraph post gets broken at a point against a storm and its top touches the ground at a distance 20 m from the base of the post making an angle 30∘ with the ground. What is the height of the post ?
View Solution
Knowledge Check
- Question 1 - Select One
The top of a broken tree has its top touching the ground (shown in the adjoining figure) at a distanc of 10 m from thee bottom. If the angle made by the broken part with ground is 30∘, then the length of the broken part is
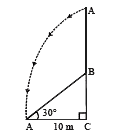
(a)10√3 cm
(b)20√3 cm
(c)20 cm
(d)20√3 mA10√3 cmB20√3 cmC20 cmD20√3 m - Question 2 - Select One
The upper part of a tree, broken by the wind makes an angle of 60° with the ground and the distance from the roots to the point where the top of the tree meets the ground is 20 m. The length of the broken part of the tree is
A20 mB40 mC20√3 mD40√3 m - Question 3 - Select One
A tree is broken by wind, its upper part touches the ground at a point 10 m from the foot of the tree and makes an angle of 60° with the ground. The entire length of the tree is
A15 mB20 mC(10+203)√3mD(10+√32) m
Due to a storm the upper part of a tall tree broke and got bent .It's top struck the ground at a distance of 8 m from its base making an angle of 30 degrees with the ground .What was the height of the tree ?
View SolutionThe upper part of a tree broken by the wind makes an angle of 60∘ with the ground and the distance from the foot to the point where the top of the tree meets the ground is 20m. What was the height of the tree?
View SolutionA tree is broken by wind, its upper part touches the ground at a point 10 metres from the foot of the tree and makes an angle of 45∘ with the ground . The entire length of the tree is
View SolutionA tree is broken by wind, its upper part touches the ground at a point 10 metres from the foot of the tree and makes an angle of 45∘ with the ground . The entire length of the tree is
View SolutionThe top of a partially broken tree touches the ground at a point 10 m from the foot of it and makes an angle of elevation of 30∘ from the ground. The height of the
View Solution

