O is the centre of a circle of diameter 4 cm and OABC the square, if the shaded area is 1/3 area of the square then the side of the square is
π√3cm
√3πcm
3√πcm
3πcm
The correct Answer is:B
Step by step video & image solution for O is the centre of a circle of diameter 4 cm and OABC the square, if the shaded area is 1/3 area of the square then the side of the square is by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Everyday Mathematics
5 Videos
- AREAS RELATED TO CIRCLESBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Achievers Section (HOTS)
5 Videos
- ARITHMETIC PROGRESSIONS BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - ACHIEVERS SECTION (HOTS)
5 Videos
Similar Questions
Knowledge Check
The area of a rectangle is 4 times the area of a square .The length of the rectangle is 90 cm and the breadth of the rectangle is 2/3 of the square.What is the side of the square ?
A10 cmB20 cmC9 cmDNone of theseThe area of a rectangle is 4 times the area of a square. The length of the rectangle is 90 cm and the breadth of the rectangle is 2/3rd of the side of the square. What is the side of the square?
A10 cmB20 cmC15 cmDCouldn't be determinedIf the area of a circle inscribed in a square is 9πcm2 then the area of the square is
A24cm2B30cm2C36cm2D81cm2
The diameter of a circle is equal to the side of the square. What is the area of the square if the area of the circle is 36 pi sq cm.
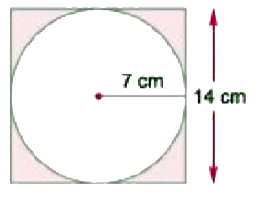
View SolutionFind the area of shaded portion if each side of the square is 14 cm.
View SolutionA circle and a square have same area. The ratio of the side of the square to the radius of the circle will be :
View SolutionIf the area of a circle inscribed in a square is 9πcm2 , then the area of the square is
View SolutionA circle and a square have same area. The ratio of the side of the square to the radius of the circle will be :
View Solution
