A chord of a circle subtends an angle of at the centre. If the length of the chord is 100 cm, then find the area of the major segment.
The correct Answer is:D
To find the area of the major segment of a circle subtended by a chord of length 100 cm at an angle of 60∘ at the center, we can follow these steps:
Step 1: Find the radius of the circle
Given that the chord subtends an angle of 60∘ at the center and the length of the chord (AB) is 100 cm, we can use the formula for the length of the chord:
AB=2rsin(θ2)
where θ is the angle subtended at the center in degrees.
Substituting the values:
100=2rsin(602)=2rsin(30)
Since sin(30)=12:
100=2r⋅12=r
Thus, the radius r=100 cm.
Step 2: Calculate the area of the sector
The area of the sector formed by the angle θ is given by:
Area of sector=θ360×πr2
Substituting θ=60∘ and r=100 cm:
Area of sector=60360×π×(100)2
=16×π×10000
=10000π6≈5233.33 cm2(using π≈3.14)
Step 3: Calculate the area of triangle OAB
Since triangle OAB is an equilateral triangle (as both OA and OB are radii and the angle AOB is 60∘), we can use the formula for the area of an equilateral triangle:
Area of triangle=√34a2
where a is the length of the side (which is equal to the radius):
Area of triangle=√34(100)2=√34×10000
≈17324≈433.00 cm2
Step 4: Calculate the area of the minor segment
The area of the minor segment is given by:
Area of minor segment=Area of sector−Area of triangle
=5233.33−433.00≈4800.33 cm2
Step 5: Calculate the area of the major segment
The area of the major segment is given by:
Area of major segment=Area of circle−Area of minor segment
The area of the circle is:
Area of circle=πr2=π×(100)2=31400 cm2
Thus,
Area of major segment=31400−4800.33≈26600 cm2
Final Answer
The area of the major segment is approximately 26600 cm2.
Given that the chord subtends an angle of 60∘ at the center and the length of the chord (AB) is 100 cm, we can use the formula for the length of the chord:
AB=2rsin(θ2)
where θ is the angle subtended at the center in degrees.
100=2rsin(602)=2rsin(30)
Since sin(30)=12:
100=2r⋅12=r
Thus, the radius r=100 cm.
The area of the sector formed by the angle θ is given by:
Area of sector=θ360×πr2
Substituting θ=60∘ and r=100 cm:
Area of sector=60360×π×(100)2
=16×π×10000
=10000π6≈5233.33 cm2(using π≈3.14)
Since triangle OAB is an equilateral triangle (as both OA and OB are radii and the angle AOB is 60∘), we can use the formula for the area of an equilateral triangle:
Area of triangle=√34a2
where a is the length of the side (which is equal to the radius):
Area of triangle=√34(100)2=√34×10000
≈17324≈433.00 cm2
The area of the minor segment is given by:
Area of minor segment=Area of sector−Area of triangle
=5233.33−433.00≈4800.33 cm2
The area of the major segment is given by:
Area of major segment=Area of circle−Area of minor segment
The area of the circle is:
Area of circle=πr2=π×(100)2=31400 cm2
Thus,
Area of major segment=31400−4800.33≈26600 cm2
The area of the major segment is approximately 26600 cm2.
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 2 EXERCISE - Everyday Mathematics10videos
IMO QUESTION PAPER 2020 SET 2
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 2 EXERCISE - Achievers Section4videos
IMO QUESTION PAPER 2020 SET 2
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 1EXERCISE - Achievers Section5videos
IMO QUESTION PAPER 2020 SET 1
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - ACHIEVERS SECTION (HOTS)5videos
INTRODUCTION TO TRIGONOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
The chord of a circle of radius 10cm subtends a right angle at its centre. The length of the chord (in cm) is
A5√2B5√2C10√2D10√3 - Question 2 - Select One
A chord of a circle of radius 28 cm makes an angle of 90∘ at the centre. Find the area of the major segment.
A1456 cm2B1848 cm2C392 cm2D2240 cm2
A chord of a circle of radius 30 cm makes an angle of 60∘ at the centre of the circle. Find the areas of the major segment. [Take π=3.14 and √3=1.732]
View SolutionA chord of a circle of radius 30 cm makes an angle of 60∘ at the centre of the circle. Find the areas of the minor and major segments. [Take π=314 and √3=1.732]
View SolutionA chord of a circle of radius 20 cm subtends an angel 90∘ at the centre. Complete the following activity to find the area of minor segment as well as major segment. (π=3.14)
View SolutionA chord of length 10 cm subtends an angle of 120∘ at the centre of the circle. Find the distance of the chord from the centre.
View SolutionA chord PQ of a circle with radius 15 cm subtends an angle of 60∘ with the centre of the circle. Find the area of the minor as well as the major segment. (π=3.14,√3=1.73)
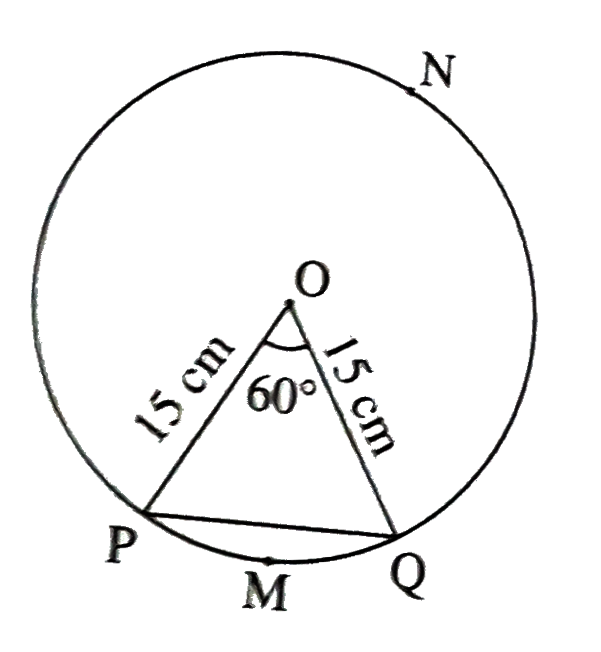 View Solution
View SolutionThe chord of a circle of radius 8 cm subtends a right angle at its centre. Find the length of the chord.
View Solution

