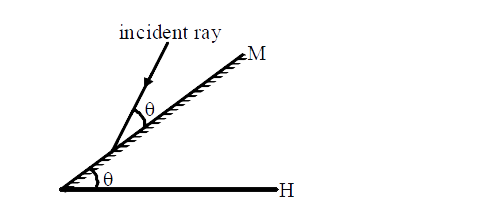
Prove that when a reflecting surface of light is tilted by an angle θ , the reflected light will be tilted by an angle 2θ
For the reflecting surface AB, the incident ray IO and the reflected ray OR1 subtend angle i with the normal N as angle of incidence is equal to angle of reflection as shown in figure . When the surface AB is tilted to A. B. by an angle θ the normal ′ N. is also is tilted by the same angle θ. Remember the position of incident ray IO remains unaltered. But, in the tilted system the angle of incidence is now i+θ and the angle of reflection is also i+θ. Now, OR2 is the reflected ray. The angle between OR2 and OR1 is,
∠A1OR2=∠N.OR2−∠NOR1
(i+θ)−(i−θ)=2θ.

Topper's Solved these Questions
- OPTICSBook:NCERT TAMILChapter:OPTICSExercise:EVALUATION (Multiple choice questions)
Explore 20 Videos
- OPTICSBook:NCERT TAMILChapter:OPTICSExercise:EVALUATION (Numerical Problems)
Explore 10 Videos
- NUCLEIBook:NCERT TAMILChapter:NUCLEIExercise:ADDITIONAL EXERCISES
Explore 9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT TAMILChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:EXERCISES
Explore 40 Videos
Similar Questions
When light of a certain wavelength is incident on a plane surface of a material at a glancing angle 30∘, the reflected light is found to be completely plane polarized Determine
Angle of refraction.
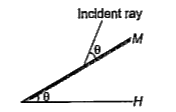
View SolutionA mirror is inclined at an angle of θ with the horizontal. If a ray of light is incident at an angle of incidence θ then the reflected ray makes the following angle with the horizontal
View Solution
Knowledge Check
When a mirror is rotated by a angle θ , the reflected ray will rotated by
A0∘Bθ/2CθD2θA light beam is being reflected by using two mirrors, as in a periscope used in submarines. If one of the mirrors rotates by an angleθ , the reflected light will be deviate from its original path by the angle :
A2θB0∘CθD4θA light beam is being reflected by using two mirrors, as in a periscope used in submarines. If one of the mirrors rotates by an angleθ , the reflected light will be deviate from its original path by the angle :
A2θB0∘CθD4θ
Show that a ray of light reflected from a plane mirror rotates througha an angle 2θ when the
mirror is rotated through an angle θ about its axis perpendicular to both the incident ray and
the normal to the surface.
View SolutionShow that a ray of light reflected from a plane mirror rotates througha an angle 2θ when the
mirror is rotated through an angle θ about its axis perpendicular to both the incident ray and
the normal to the surface.
View SolutionLight of wavelength 6000Å falls on a plane reflecting surface. What are the wavelength and frequency of reflected light. If angle between incident ray and reflected ray is 60∘, what is the angle of incidence ?
View SolutionA light beam is being reflected by using two mirrors, as in a periscope used in submarines. If one of the mirrors rotates by an angle θ, the reflected light will deviate from its original path by the angle
View SolutionA mirror is inclined at an angle of θ with the horizontal. If a ray of light is incident at an angle in incidence θ then the reflected ray will make the angle with horizontal, is
View Solution
