Question

A thin rod of length f/3 is placed along the optical axis of a concave mirror of focal length f such that its image which is real and elongated just touches the rod. Calculate the longitudinal.

Explanation

longitudinal magnification `(m)=("lengthof image (l.)")/("lengthof object (l)")`
Given: length of object, `l=(f)/(3)`

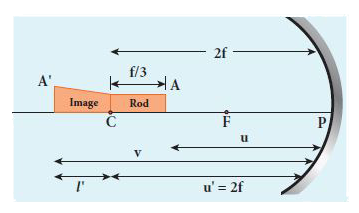
Let, l be the length of the image, then,
`m=(l.)/(l)=(l.)/(f//3)" (or) "l=(mf)/(3)`
Image of one end coincides with the object. Thus, the coinciding end must be at center of curvature.
Hence, `u.=R=2f`
`u.=u+(f)/(3)`
`u=u.-(f)/(3)=2f-(f)/(3)=(5f)/(3)`
`v=u+(f)/(3)+(mf)/(3)=(5f)/(3)+(f)/(3)+(mf)/(3)=(f(6+m))/(3)`
Mirror equation, `1/v+1/u=1/f`
`(1)/(-(f(6+m))/(3))+(1)/(-((5f)/(3)))=(1)/(-f)`
After simplifying,
`(3)/(f(6+m))+(3)/(5f)=(1)/(f),(3)/((6+m))=(2)/(5)`
`6+m=(15)/(2),m=(15)/(2)-6`
`m=(3)/(2)=1.5`.