The thickness of a glass slab is 0.25 m. it has a refractive index of 1.5. A ray of light is incident on the surface of the slab at an angle of 60∘ . Find the lateral displacement of the light when it emerges from the other side of the mirror.
Given, thickness of the lab, t=0.25 m refractive index, n=1.5, angle of incidence i=60∘.
Using Snell’s law, 1×sini=nsinr
sinr=sinin=sin601.5=0.58
r=sin−10.58=35.25∘
Lateral displacement is, L=t(sin(i−r)cos(r))
L=(0.25)×(sin(60−35.25)cos(35.25))=0.1281m
The lateral displacement is, L=12.81 cm
Topper's Solved these Questions
- OPTICSBOOK - NCERT TAMILCHAPTER - OPTICSEXERCISE - EVALUATION (Multiple choice questions)
20 Videos
- OPTICSBOOK - NCERT TAMILCHAPTER - OPTICSEXERCISE - EVALUATION (Numerical Problems)
10 Videos
- NUCLEIBOOK - NCERT TAMILCHAPTER - NUCLEIEXERCISE - ADDITIONAL EXERCISES
9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT TAMILCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISES
40 Videos
Similar Questions
A ray of light is incident on a surface of glass slab at an angle 45∘. If the lateral shift produced per unit thickness is 1/√3, the angle of refraction produced is
View SolutionA ray of light is incident on a 60∘ glass prism at an angle of 60∘. Find the
the angle of emergence
the angle of deviation, given the refractive index of glass = 1.5.
View Solution
Knowledge Check
A ray of light is incident on a surface of glass slab at an angle 45∘. If the lateral shift produced per unit thickness is 1/√3, the angle of refraction produced is
Atan−1(√32)Btan−1(1−√23)Csin−1(1−√23)Dtan−1(√23−1)Maximum lateral displacement of ray light incident on a slab of thickness t is
At2Bt3Ct4DtA ray of light is incident on a glass slab at an angle of 45∘. If refractive index of glass be 1.6, what is the angle of refraction ?
A45.2∘B30∘C26.2∘D15.2∘
A parallel sides glass slab of thickness 4 cm is made of a material of refractive index √3. When light is incident on one of the parallelfaces at an angle of 60∘ , it emerges from the other parallel face. Find the lateral displacement of the emergent beam.
View SolutionOne side of a glass slab is silvered as shown in the figure. A ray of light is incident on the other side at angle of incidence 45∘. Refractive index of glass is given as √2. The deflection suffered by the ray when it comes out of the slab is
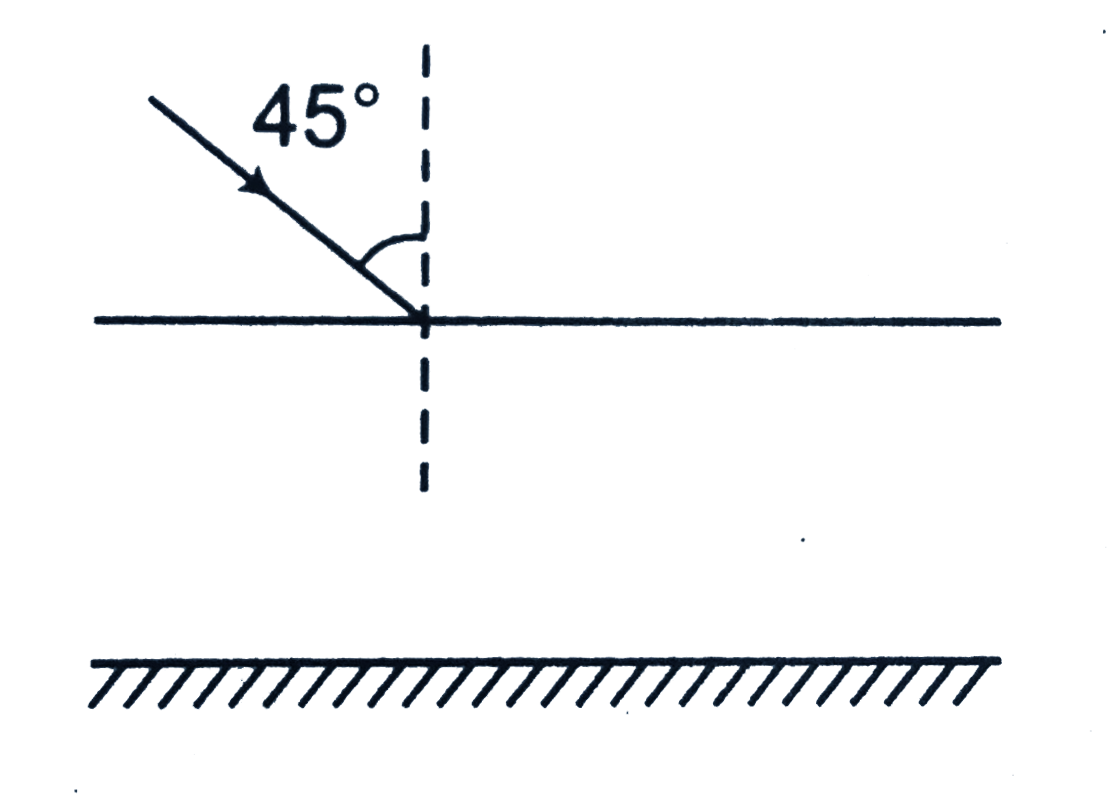
View SolutionA ray of light is incident on a glass slab making an angle of 30∘ with the surface. The angle of refraction in glass, if the refractive index of flass is 1.6 , is
View SolutionA ray of light is incident on a glass slab of refractive index 1.5, making an angle of 40∘ with the surface. The angle of refraction in glass is
View SolutionOne side of a glass slab is silvered as shown in the figure. A ray of light is incident on the other side at angle of incidence 45∘. Refractive index of glass is given as √2. The deflection suffered by the ray when it comes out of the slab is

View Solution
