Light of wavelength 500 nm passes through a slit of 0.2 mm wide. The diffraction pattern is formed on a screen 60 cm away. Determine the,
the distance between the central maximum and the second minimum.

Text Solution

Verified by Experts

$λ = 500 nm = 500 \times 10^{- 9} m, a = 0.2 mm = 0.2 \times 10^{- 3} m, D = 60 cm = 60 \times 10^{- 2} m$
To find the value of $y_{1}$ for central maximum, which is spread up to first minimum with (n=1) is, $a sin θ = λ$
As $θ$ is very small, $sin θ \approx tan θ = \frac{y_{1}}{D}$
$a \frac{y_{1}}{D} = λ$ rewriting, $y_{1} = \frac{λ D}{a}$
Substituting,
$y_{1} = \frac{500 \times 10^{- 9} \times 60 \times 10^{- 2}}{0.2 \times 10^{- 3}} = 1.5 \times 10^{- 3} = 1.5 mm$
To find the value of y2 for second minimum with (n=2) is, $a sin θ = 2 λ$
$a \frac{y_{2}}{D} = 2 λ rewriting, y_{2} = \frac{2 λ D}{a}$
Substituting,
$y_{2} = \frac{2 \times 500 \times 10^{- 9} \times 60 \times 10^{- 2}}{0.2 \times 10^{- 3}} = 3 \times 10^{- 3} = 3 mm$
The distance between the central maximum and second minimum is, $y_{2} - y_{1}$
$y_{2} - y_{1} = 3 mm - 1.5 mm = 1.5 mm$

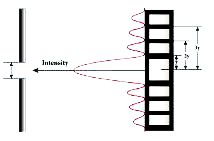
Note: The above calculation shows that in the diffraction pattern caused by single slit, the width of each maximum is equal with central maximum as the double that of others. But the bright and dark fringes are not of equal width.

Updated on:21/07/2023