A monochromatic light of wavelength 5000 Å passes through a single slit producing diffraction pattern for the central maximum as shown in the figure. Determine the width of the slit.
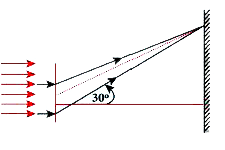
λ=5000Å=5000×10−10m,sin30∘=0.5,
n=1,a=?
Equation for diffraction minimum is, asinθ=nλ
The central maximum is spread up to the first minimum. Hence, n = 1
Rewriting, a=λsinθ
Substituting, a=5000×10−100.5
a=1×10−6m=0.001×10−3m=0.001 mm
Topper's Solved these Questions
- OPTICSBOOK - NCERT TAMILCHAPTER - OPTICSEXERCISE - EVALUATION (Multiple choice questions)
20 Videos
- OPTICSBOOK - NCERT TAMILCHAPTER - OPTICSEXERCISE - EVALUATION (Numerical Problems)
10 Videos
- NUCLEIBOOK - NCERT TAMILCHAPTER - NUCLEIEXERCISE - ADDITIONAL EXERCISES
9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT TAMILCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISES
40 Videos
Similar Questions
In a single slit diffraction pattern, how does the angular width of central maxima change when slit width is decreased
View SolutionParallel light of wavelength 5000 Å falls normally on a single slit. The central maximum spreads out to 30∘ on either side of the incident light.Find the width of the slit.For what width of the slit the central maximum would spread out to 90∘ from the direction of the incident light ?
View Solution
Knowledge Check
The first minimum of a single slit diffraction pattern is observed at angle 2∘ with a light of wavelength 698 nm. The width of this slit is
A2 mmB0.2 mmC0.02 mmD0.002 mmFor a parallel beam of monochromatic light of wavelength 'λ' diffraction is produced by a single slit whose width 'a' is of the order of the wavelength of the light. If 'D' is the distance of the screen from the slit, the width of the central maxima will be
A(a) 2DλaB(b) DλaC(c) DaλD(d) 2DaλFor a parallel beam of monochromatic. Light of wavelength 'λ' diffraction is produced by a single slit whose width 'a' is of the order of the wavelength of the lightl. If 'D' is the distance of the screen from the slit, the width of the central maxima will be
A2DλaBDλaCDaλD2Daλ
Parallel light of wavelength 5000 Å falls normally on a single slit. The central maximum spreads out to 30∘ on either side of the incident light.Find the width of the slit.For what width of the slit the central maximum would spread out to 90∘ from the direction of the incident light ?
View SolutionLight of wavelength 6,000Å falls on a single slit and diffracts. It is observed that the first maximum in diffraction pattern subtends an angle of 45∘. Calculate the slit width.
View Solution(a) Derive the relation asinθ=λ for the first minimum of the diffraction pattern produced due to a single-slit of width 'a' using light of wavelength λ.
(b) State with reason, how the linear width of central maximum will be affected if (i) monochromatic yellow light is replaced with red light, and (ii) distance between the slit and the screen is increased.
(c) using the monochromatic light of same wavelength in the experimental set-up of the diffraction pattern as well as in the interference pattern where the slit separation is 1mm, 10 interference fringes are found to be within the central maximum of the diffraction pattern. determine the width of the single-slit, if the screen is kept at the same distance from the slit in the two cases.
View Solution(a) Derive the relation a sinθ=λ for the first minimum of the diffraction pattern produced due to a single slit of width ‘a’ using light of wavelengthλ.
(b) State with reason, how the linear width of central maximum will be affected if
(i) monochromatic yellow light is replaced with red light, and
(ii) distance between the slit and the screen is increased.
(c) Using the monochromatic light of same wavelength in the experimental set-up of the diffraction pattern as well as in the interference pattern where the slit separation is 1 mm, 10 interference fringes are found to be within the central maximum of the diffraction pattern. Determine the width of the single slit, if the screen is kept at the same distance from the slit in the two cases.
View SolutionFor a parallel beam of monochromatic light of wavelength 'λ' diffraction is produced by a single slit whose width 'a' is of the order of the wavelength of the light. If 'D' is the distance of the screen from the slit, the width of the central maxima will be
View Solution
