Doubtnut Promotions Sticky

Eddy current loss is directly proportional to (f= frequency B_(m)= maximum flux density)(a)f^(2) and B2m (b) f and Bm (c) fand B2m (d) f2 and Bm

Video Solution
|
Answer

Step by step video & image solution for Eddy current loss is directly proportional to (f=" frequency " "B_(m)= maximum flux density")(a) f^(2) and B_(m)^(2) (b) f and B_(m) (c) fand B_(m)^(2) (d) f^(2) and B_(m) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12PHYSICSALTERNATING CURRENT

Similar Questions

Knowledge Check

  • Question 1 - Select One

    If ab=cd=ef=4, then
    m2a+n2c+p2em2b+n2d+p2f=?

    A1
    B4
    C8
    D16
  • Question 2 - Select One

    Let y=f(x) be a twice differentiable, non- negative function defined on [a.b]. The area ∫baf(x)dx,b> a bounded by y=f(x), the x-axis and the ordinates at x=aandx=b can be approximated as
    ∫baf(x)dx≈(b−a)2{f(a)+f(b)}.
    Since ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx,xˆI(a,b),a better approximation to ∫baf(x)dx can be written as ∫baf(x)dx@(c−a)2{f(a)+f(c)}(b−c)2
    {f(c)+f(b)}∘F(c),
    If c=b−a2, then this gives:
    ∫baf(x)dx@b−a4{f(a)+2f(a)+2f(c)+f(b)},.......(1)
    If f''(x)<0,x∈(a,b), then at the point
    C(c,f(c))ony=f(x) for which F(c ) is a maximum,
    f'(c) is given by

    Af'(c)f(b)−f(a)b−a
    Bf'(c)f(b)−f(a)a−b
    Cf'(c)=2(f(b)−f(a))b−a
    Df'(c)=0
  • Question 3 - Select One

    Three particles A, B and C of mass m, m and 2m lie in a straight line as shown. The only force acting on these particles is due to the gravitational attraction towards each other. Let the magnitude of net force on them be FA,FB and FC respectively. Then,FA:FB:FC is equal to :
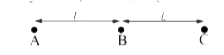    ocr_image

    A3:2:5
    B3:1:4
    C2:2:3
    D6:1:5