The energy E of an oscillating body in simple harmonic motion depends on its mass m, frequency n and amplitude A as E= k(m)x(n)y(A)z.Find the value of (2x+y+z) [Amplitude is distance]
Step by step video solution for The energy E of an oscillating body in simple harmonic motion depends on its mass m, frequency n and amplitude A as E= k(m)^(x)(n)^(y)(A)^(z).Find the value of (2x+y+z) [Amplitude is distance] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023সম্পর্কিত প্রশ্ন
The energy E of an oscillating body is simple harmonic motion depends on its mass m, frequency n and emplitude a using the method of dimensional analysis find the relation between E ,m, n and a .
View SolutionA body is executing simple harmonic motion with frequency 'n' the frequency of its potential energy is
View Solution
জ্ঞান পরীক্ষা করুন
The mass M shown in the figure oscillates in simple harmnonic motion and amplitude A. The amplitude of the point P is
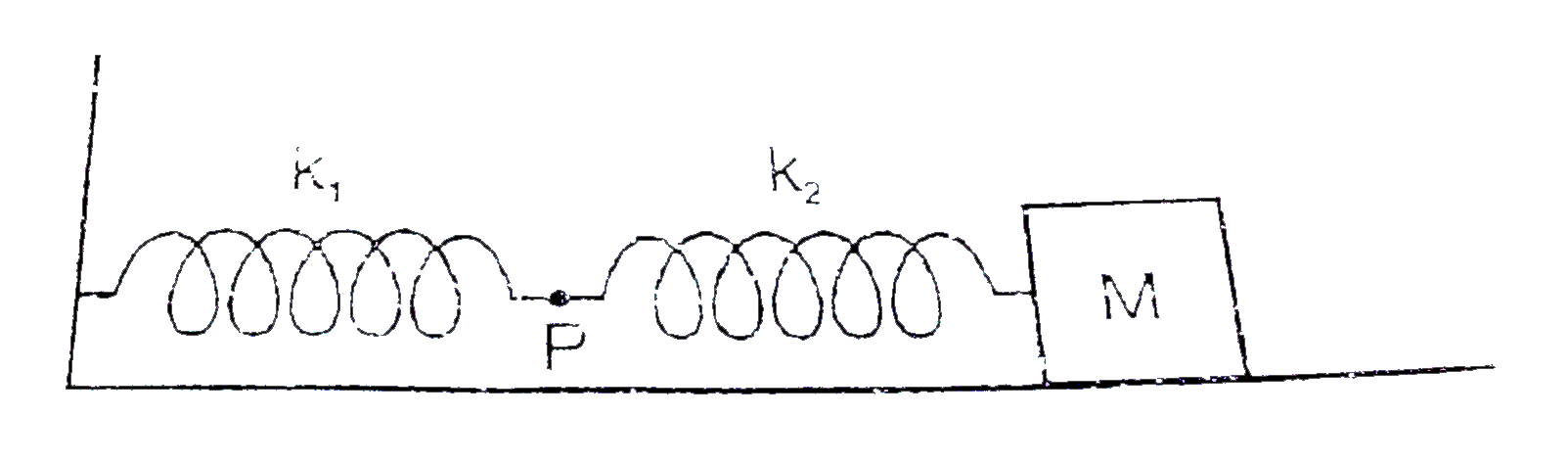 Ak1Ak2Bk2Ak1Ck1Ak1+k2Dk2Ak1+k2
Ak1Ak2Bk2Ak1Ck1Ak1+k2Dk2Ak1+k2The amplitude of given simple harmonic motion is y=(3sinωt+4cosωt)m
A1 mB3 mC4 mD5 mThe mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
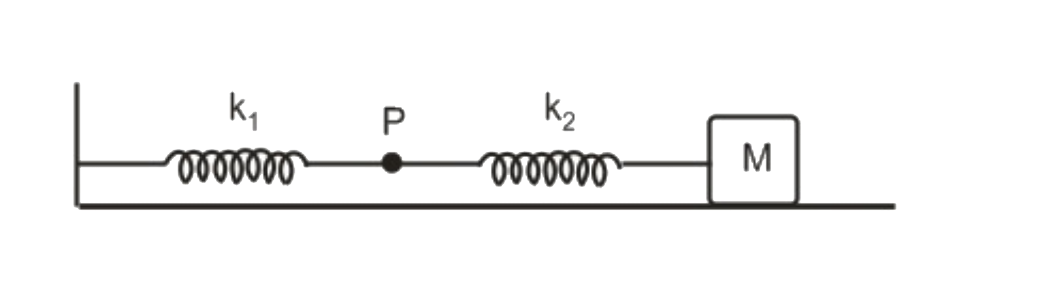 Ak1Ak2Bk2Ak2−k1Ck2Ak1+k2Dk2Ak1
Ak1Ak2Bk2Ak2−k1Ck2Ak1+k2Dk2Ak1
A mass m oscillates with simple harmonic motion with frequency f=ω2πand amlitude A on a spring with constant K. therefore
View SolutionA linear harmonic oscillator of force constant 106N/m and amplitude 2 cm has
View SolutionAverage energy in one time period of a simple harmonic oscillator whose amplitude is A, angular velocity ,ω and mass m , is
View SolutionThe total mechanical energy of a particle executing simple harmonic motion is E when the displacement is half the amplitude of its kinetic energy will be
View SolutionA body is executing simple harmonic motion with an angular frequency s rad/2 . The velocity of the body at 20 mm displacement, when the amplitude of motion is 60 mm , is
View Solution