Consider a particle of charge q describing a closed orbit like that of an electron in an atom.The angular momentum of the particle L and the magnetic dipole moment M of the corresponding current loop are related as (m− is the mass of a charged particle)
Step by step video & image solution for Consider a particle of charge q describing a closed orbit like that of an electron in an atom.The angular momentum of the particle L and the magnetic dipole moment M of the corresponding current loop are related as (m- is the mass of a charged particle) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle of charges Q and mass m travels through a potential difference V from rest. The final momentum of the particle is
AmvQB2Q√mVC√2mQVD√2QVm - Question 2 - Select One
A particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about P?
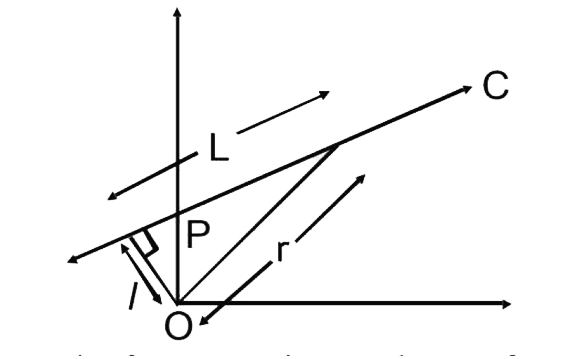 AmvLBmvICmvrDzero
AmvLBmvICmvrDzero - Question 3 - Select One
A particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 AmvLBmvlCmvrDzero
AmvLBmvlCmvrDzero
Centripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?
View SolutionA particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA charged particle of mass m and charge q is released from rest the position (x0,0) in a uniform electric field E0ˆj. The angular momentum of the particle about origin.
View SolutionA particle of mass m is describing a circular path of radius r with uniform speed. If L is the angular momentum of the particle (about the axis of the circle), then the kinetic energy of the particle is given by
View Solution
