किसी विद्युत परिपथ में प्रतिरोध R1 व R2 समांतर क्रम में जुड़े होने पर सिद्ध कीजिये कि तुल्य प्रतिरोध REQ=R1R2R1+R2
Step by step video & image solution for किसी विद्युत परिपथ में प्रतिरोध R_1 व R_2 समांतर क्रम में जुड़े होने पर सिद्ध कीजिये कि तुल्य प्रतिरोध R_EQ = (R_1 R_2 )/(R_1 + R_2) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
स्तंभ 'अ' के प्रत्येक कथन के लिये स्तंभ'ब' में से उपयुक्त विकल्प चुनकर सही जोड़े बनाइये
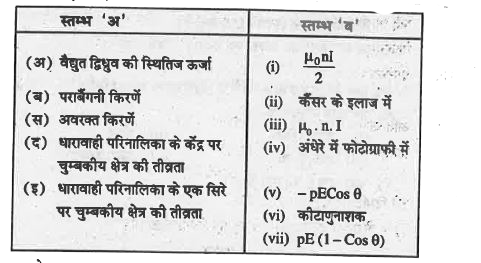
View Solutionज्वलनशील पदार्थों को ले जानेवाली गाड़ियों से जंजीरे जमीन को छूती हुई लगाई जाती है। क्यों?
View SolutionFor any three non-zero vectors r_1,r_2 and r_3 .|(r_1.r_1,r_1.r_2,r_1.r_3),(r_2.r_1,r_2.r_2,r_2.r_3),(r_3.r_1,r_3.r_2,r_3.r_3)|=0. Then which of the following is false
View SolutionIn ΔABC,r3+r1r2r1+r2=
View SolutionIn ΔABC,r1r2√[4R−r1−r2r1+r2]
View SolutionIn ΔABC,r2(r3+r1)√r1r2+r2r3+r3r1=
View SolutionIn the given loop the magnetic field at the centre O is 1) (mu_0I)/(4) ( (r_1 + r_2)/(r_1 r_2) ) out of the page 2) (mu_0I)/(4) ( (r_1 + r_2)/(r_1 r_2)) into the page 3) (mu_0I)/(4) ( (r_1 - r_2)/(r_1 r_2)) out of the page 4) (mu_0 I)/(4) ( (r_1 - r_2)/(r_1r_2) ) into the page
View Solutionকোনাে তড়িৎবর্তনীতে e তড়িৎচালক বলবিশিষ্ট দুটি তড়িৎকোশকে শ্রেণি সমবায়ে বহিস্থ R রােধের সাথে যুক্ত করা হল কৌশদ্বয়ের অভ্যন্তরীণ রােধ যথাক্রমে r1এবং r2 | প্রবাহ চলাকালীন যদি প্রথম কোশের বিভবপার্থক্য শূন্য হয় তবে R এবং r1 ও r2 এর মধ্যে সম্পর্ক হবে R=r1+r2 R=r1−r2 R=½(r_1+r_2) R=½(r1−r2)
View SolutionΔ=r1r2√4R−r1−r2/r1+r2 అని చూపండి.
View Solutionr1r2+r3√r1r2+r2r3+r3r1=a అని రుజువు చేయండి.
View SolutionThe magnitudes of the gravitational fields at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively then
(a)F1F2=r1r2 if r1<R and r2<R
(b)F1F2=(r2r1)2 if r1>R and r2>R
(c)F1F2=r1r2 if r1>R and r2>R
(d)F1F2=(r1r2)2 if r1<R and r2<R
View SolutionIf (r2−r1)(r3−r1)=2r2r3. show that A=90∘
(1−r1r2)(1−r1r3)=2 , show that A=90∘
View SolutionIn ΔABC,r1r2√[4R−r1−r2r1+r2]=
View Solution( r_1+ r_2) (r_2+r_3) (r_3+r_1) =
View Solutionr1(r2+r3)√r1r2+r2r3+r1r3=
View SolutionShow that ab−r1r2r3=bc−r2r3r1=ca−r3r1r2
View Solution
